考点:异面直线及其所成的角,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)由已知条件推导出四边形ADB1D1为平行四边形,从而得到AD1∥平面CDB1,同理,C1D1∥平面CDB1,由此能证明平面AC1D1∥平面CDB.
(2)由线面垂直得AA1⊥CD.∵由等腰三角形性质得CD⊥AB,从而得到CD⊥平面ABB1A1,由此能证明平面CDB1⊥平面ABB1A1.
(3)连接BC1交B1C于E,连接DE,取AA1中点F,连接EF,由已知条件推导出∠EDF是异面直线AC1与A1B所成的角.由此能求出异面直线AC1与A1B所成的角.
解答:

(1)证明:在直三棱柱ABC-A
1B
1C
1中,
∵点D,D
1分别是AB,A
1B
1的中点,D
1B
1∥AD,
∴四边形ADB
1D
1为平行四边形,
∴AD
1∥DB
1,∵AD
1?平面CDB
1,∴AD
1∥平面CDB
1,
同理,C
1D
1∥平面CDB
1,
∵AD1∩D
1C
1=D
1,
∴平面AC
1D
1∥平面CDB.(4分)
(2)证明:∵AA
1⊥平面ABC,CD?平面ABC,
∴AA
1⊥CD.∵AC=BC,D是AB的中点,
∴CD⊥AB,∵AA
1∩AB=A,∴CD⊥平面ABB
1A
1,
∵CD?平面ABC,
∴平面CDB
1⊥平面ABB
1A
1.(9分)
(3)解:连接BC
1交B
1C于E,连接DE,
取AA
1中点F,连接EF,又∵D是AB中点,
∴AC
1∥DE,DF∥A
1B,
∴∠EDF是异面直线AC
1与A
1B所成的角.
设AC=DE=
,DF=
=,EF=
,
∴DE
2+DF
2=EF
2,∴∠EDF=90°,
∴异面直线AC
1与A
1B所成的角为90°.(13分)
点评:本题考查平面与平面垂直的证明,考查平面与平面垂直的证明,考查异面直线的成的角的求法,解题时要注意空间思维能力的培养.

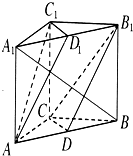 如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC,AA1⊥平面ABC,点D,D1分别是AB,A1B1的中点. (1)证明:在直三棱柱ABC-A1B1C1中,
(1)证明:在直三棱柱ABC-A1B1C1中,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD= 在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是直角梯形,AB∥CD,∠BAD=90°,AB=AD=PD=1,CD=2.