
分析 (Ⅰ)由题意可得c=1,由直线和圆相切的条件:d=r,可得b=1,进而得到a,即有椭圆方程;
(Ⅱ)(i)设A(x1,y1),B(x2,y2),将直线方程代入椭圆方程,运用判别式大于0,以及韦达定理,结合直线的斜率公式,可得m=-2k,进而得到直线恒过定点(2,0);
(ii)由直线l的斜率是直线OA,OB斜率的等比中项,即有k2=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$,运用韦达定理,可得k,再由点到直线的距离公式和弦长公式,运用三角形的面积公式,结合基本不等式可得面积的最大值,即有面积的取值范围.
解答 解:(Ⅰ)由题意可得c=1,即a2-b2=1,
由直线3x-4y+5=0与圆x2+y2=b2相切,
可得b=$\frac{|0-0+5|}{\sqrt{9+16}}$=1,解得a=$\sqrt{2}$,
即有椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)(i)证明:设A(x1,y1),B(x2,y2),
将直线y=kx+m(m≠0)代入椭圆x2+2y2=2,
可得(1+2k2)x2+4kmx+2m2-2=0,
即有△=16k2m2-8(1+2k2)(m2-1)>0,
x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-2}{1+2{k}^{2}}$,
由k1+k2=$\frac{{y}_{1}}{{x}_{1}-1}$+$\frac{{y}_{2}}{{x}_{2}-1}$=$\frac{k{x}_{1}+m}{{x}_{1}-1}$+$\frac{k{x}_{2}+m}{{x}_{2}-1}$=0,
即有2kx1x2-2m+(m-k)(x1+x2)=0,
代入韦达定理,可得2k•$\frac{2{m}^{2}-2}{1+2{k}^{2}}$-2m+(m-k)(-$\frac{4km}{1+2{k}^{2}}$)=0,
化简可得m=-2k,
则直线的方程为y=kx-2k,即y=k(x-2),
故直线l恒过定点(2,0);
(ii)由直线l的斜率是直线OA,OB斜率的等比中项,
即有k2=$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$,即为k2x1x2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2,
可得m2+km(-$\frac{4km}{1+2{k}^{2}}$)=0,
解得k2=$\frac{1}{2}$,
代入△=16k2m2-8(1+2k2)(m2-1)>0,
可得-$\sqrt{2}$<m<$\sqrt{2}$,且m≠0.
由O到直线的距离为d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$,
弦长AB为$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{2}$$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{1+2{k}^{2}-{m}^{2}}}{1+2{k}^{2}}$,
则△OAB面积为S=$\frac{1}{2}$d|AB|=$\sqrt{2}$•$\frac{\sqrt{{m}^{2}(2-{m}^{2})}}{2}$≤$\frac{\sqrt{2}}{2}$•$\frac{{m}^{2}+2-{m}^{2}}{2}$=$\frac{\sqrt{2}}{2}$,
当且仅当m2=2-m2,即m=±1时,取得最大值.
则△OAB面积的取值范围为(0,$\frac{\sqrt{2}}{2}$].
点评 本题考查椭圆的方程的求法,注意运用直线与圆相切的条件:d=r,考查直线恒过定点的求法,注意运用联立直线方程和椭圆方程,运用韦达定理和直线的斜率公式,考查三角形的面积的范围,注意运用等比数列的中项的性质和韦达定理及弦长公式,以及点到直线的距离公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
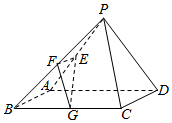 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,A,B,C,D为平面四边形ABCD的四个内角.
如图,A,B,C,D为平面四边形ABCD的四个内角.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
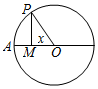 如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )
如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )| A. | 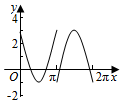 | B. |  | C. | 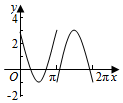 | D. | 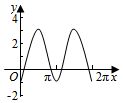 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com