
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;
如图,矩形ABCD所在平面与直角梯形CDEF所在平面互相垂直,其中∠EDC=∠DEF=$\frac{π}{2}$,EF=ED=$\frac{1}{2}$CD=1,AD=$\sqrt{2}$.(1)若M为AE的中点,求证:EC∥平面BDM;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
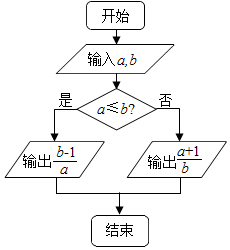
| A. | $\frac{{\sqrt{2}+1}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}-1}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
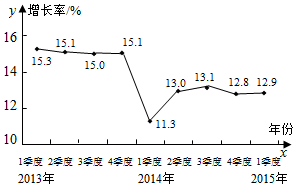 如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )
如图是近三年某市生产总值增速(累计,%)的折线统计图,据该市统计局初步核算,2015年一季度全区生产总值为1552.38亿元,与去年同一时期相比增长12.9%(如图,折线图中其它数据类同).根据统计图得出正确判断是( )| A. | 近三年该市生产总值为负增长 | |
| B. | 近三年该市生产总值为正增长 | |
| C. | 该市生产总值2013年到2014年为负增长,2014年到2015年为正增长 | |
| D. | 以上判断都不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com