
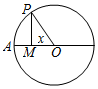
 如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )
如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )| A. | 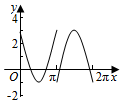 | B. |  | C. | 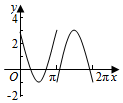 | D. | 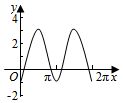 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
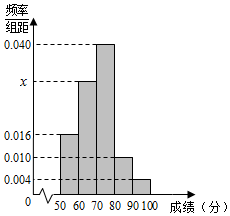 某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100]的有2人,由此推测频率分布直方图中的x=0.03.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com