
分析 由已知可得:a1=16,a1+a2=a1(1+q)=32,a1+a2+a3=${a}_{1}(1+q+{q}^{2})$=76,a1+a2+a3+a4=${a}_{1}(1+q+{q}^{2}+{q}^{3})$=130,不妨假设第一个与第二个等式成立,解得a1=16,q=1,经过验证第四个与第三个等式都不成立,因此第一个与第二个等式必定有一个不成立.假设第一个与第三个等式成立,解得a1,q.验证即可得出.
解答 解:由已知可得:a1=16,a1+a2=a1(1+q)=32,a1+a2+a3=${a}_{1}(1+q+{q}^{2})$=76,a1+a2+a3+a4=${a}_{1}(1+q+{q}^{2}+{q}^{3})$=130,
不妨假设第一个与第二个等式成立,解得a1=16,q=1,经过验证第四个与第三个等式都不成立,因此第一个与第二个等式必定有一个不成立.
假设第一个与第三个等式成立,解得a1=16,q=$\frac{3}{2}$或-$\frac{5}{2}$.经过验证q=$\frac{3}{2}$时,第四个等式成立,因此可得:算错的这个数是S2,该数列的公比是 $\frac{3}{2}$.
故答案分别为:32(S2),$\frac{3}{2}$.
点评 本题考查了等比数列的通项公式,考查了推理能力与计算能力,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
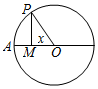 如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )
如图,圆O的半径为2,圆上一点P从A出发,绕着点O顺时针方向旋转一周,在旋转的过程中,记∠AOP为x(x∈[0,2π]),P在OA上的射影为M,记f(x)=$\overrightarrow{OP}$•$\overrightarrow{OM}$-1,那么函数f(x)的图象大致为( )| A. | 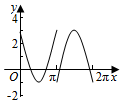 | B. |  | C. | 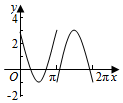 | D. | 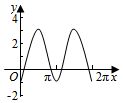 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | {-1,1} | B. | {3,5} | C. | {-1,1} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com