
分析 (I)运用离心率公式和点满足椭圆方程,解方程可得a=2,b=1,进而得到椭圆方程;
(Ⅱ)讨论直线l的斜率不存在和存在,设出直线的方程,代入椭圆方程,运用判别式大于0和韦达定理,结合向量的加法的坐标表示,化简整理解方程即可得到所求直线方程.
解答 解:(I)由题意得e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,$\frac{3}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1,a2-b2=c2,
解得a=2,b=1,
所以椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)(1)当直线l与x轴垂直时,点P(2,0),
直线l的方程为x=1满足题意;
(2)当直线l与x轴不垂直时,设直线l:y=kx+m,显然k≠0,m≠0.
设A(x1,y1),B(x2,y2),
将y=kx+m代入$\frac{x^2}{4}+{y^2}=1$.得(4k2+1)x2+8kmx+4m2-4=0,$△={(8km)^2}-4(4{k^2}+1)(4{m^2}-4)>0,{x_1}+{x_2}=\frac{-8km}{{4{k^2}+1}}$.
${y_1}+{y_2}=k({{x_1}+{x_2}})+2m=\frac{2m}{{4{k^2}+1}}$.
由直线l:y=kx+m(k≠0,m≠0),过点(1,1),得m=1-k,
因此${x_1}+{x_2}=\frac{8k(k-1)}{{4{k^2}+1}},{y_1}+{y_2}=\frac{2(1-k)}{{4{k^2}+1}}$.$\overrightarrow{OP}=\overrightarrow{OA}+\overrightarrow{OB}=({{x_1}+{x_2},{y_1}+{y_2}})=({\frac{8k(k-1)}{{4{k^2}+1}},\frac{2(1-k)}{{4{k^2}+1}}})$,
$\frac{1}{4}{({\frac{8k(k-1)}{{4{k^2}+1}}})^2}+{({\frac{2(1-k)}{{4{k^2}+1}}})^2}=\frac{{4{{(1-k)}^2}}}{{4{k^2}+1}}=1$,
4(1-k)2=4k2+1,得$k=\frac{3}{8},m=\frac{5}{8}$.满足△>0.
所以直线l的方程为$y=\frac{3}{8}x+\frac{5}{8}$.
综上,椭圆C上存在点P,使得$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OP}$成立,
此时直线l的方程为$y=\frac{3}{8}x+\frac{5}{8}$或x=1.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查直线方程的求法,注意讨论直线的斜率,以及联立直线方程和椭圆方程运用韦达定理和判别式大于0,同时考查向量加法的坐标运算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
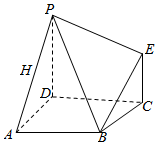 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com