
分析 (1)证法一:设x1<x2,作差判断出f(x1)<f(x2),根据函数单调性的定义,可得:f(x)是R上的增函数.
证法二:求导,根据f′(x)>0恒成立,可得:f(x)是R上的增函数.
(2)原方程可化为3-2•5x=52x,即(5x-1)(5x+3)=0,由5x+3>3≠0得:5x-1=0,解得答案.
解答 (1)证明:证法一:
设x1<x2,则${3}^{{x}_{1}}<{3}^{{x}_{2}},{3}^{{x}_{1}}-{3}^{{x}_{2}}<0,{{3}^{{x}_{1}}+1>0,3}^{{x}_{2}}+1>0$
∴f(x1)-f(x2)=$\frac{{3}^{{x}_{1}}-1}{{3}^{{x}_{1}}+1}$-$\frac{{3}^{{x}_{2}}-1}{{3}^{{x}_{2}}+1}$=$\frac{{2(3}^{{x}_{1}}-{3}^{{x}_{2}})}{{(3}^{{x}_{1}}+1){(3}^{{x}_{2}}+1)}$<0,
∴f(x1)<f(x2),
∴f(x)是R上的增函数.
证法二:f(x)=$\frac{{3}^{x}-1}{{3}^{x}+1}$=1-$\frac{2}{{3}^{x}+1}$,
∴f′(x)=$\frac{2•{3}^{x}•ln3}{({3}^{x}+1)^{2}}$,
∵f′(x)>0恒成立,
故f(x)是R上的增函数.
(2)解:由解得原方程可得3-2•5x=52x,
整理得(5x-1)(5x+3)=0,
∵5x+3>3≠0,
∴5x-1=0,
解得x=0,
∴所求方程的解集为{0}
点评 本题考查的知识点是函数单调性的证明,指数方程的解法,难度中档.


科目:高中数学 来源: 题型:填空题
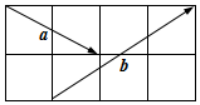 如图,在2×4的方格纸中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起点和终点均在格点的向量,则向量2$\overrightarrow a$+$\overrightarrow b$与$\overrightarrow a$-$\overrightarrow b$的夹角余弦值是$-\frac{{\sqrt{10}}}{10}$.
如图,在2×4的方格纸中,若$\overrightarrow{a}$和$\overrightarrow{b}$是起点和终点均在格点的向量,则向量2$\overrightarrow a$+$\overrightarrow b$与$\overrightarrow a$-$\overrightarrow b$的夹角余弦值是$-\frac{{\sqrt{10}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com