
分析 (1)求导函数,条件转化为a≥-$\frac{1}{2}$x2+x,x∈(0,3]恒成立,分离参数求最值,即可得出结论;
(2)分别求出直线y=(m-1)x过原点和A(1,0)的斜率以及过原点和B的斜率,从而求出m的范围即可.
解答 解:(1)∵函数f(x)=lnx+$\frac{a}{x}$,
∴f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$,
∵y=f(x)图象上任意一点的切线的斜率k≤$\frac{1}{2}$恒成立,
∴$\frac{1}{x}$-$\frac{a}{{x}^{2}}$≤$\frac{1}{2}$,x∈(0,3]恒成立,
∴a≥-$\frac{1}{2}$x2+x,x∈(0,3]恒成立,
由 y=-$\frac{1}{2}$x2+x=-$\frac{1}{2}$(x-1)2+$\frac{1}{2}$,可知x=1时,函数值为$\frac{1}{2}$,
∴a≥$\frac{1}{2}$,
∴实数a的取值范围是[$\frac{1}{2}$,+∞).
(2)a=0时,f(x)=lnx,
x=1时,f(x)=0,x=e2时,f(x)=2,
f(x)过A(1,0),B(e2,2),
由m-1=0,解得:m=1,
由m-1=$\frac{2}{{e}^{2}}$,解得:m=$\frac{{e}^{2}+2}{{e}^{2}}$,
∴m∈[1,$\frac{{e}^{2}+2}{{e}^{2}}$).
点评 题考查了导数的几何意义,函数在图象上某点处的切线的斜率就是在该点处的导数值,考查了利用分离变量法求参数的取值范围,此题是中档题.


科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
| A. | (1,2) | B. | (5,2) | C. | (2,5) | D. | (2.5,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1] | B. | (1,+∞) | C. | (-∞,-4] | D. | (-∞,-4]∪(-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
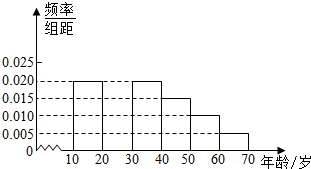 某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示
某社区为调查当前居民的睡眠状况,从该社区的[10,70]岁的人群中随机抽取n人进行一次日平均睡眠时间调查,这n人中各年龄组人数的频率分布直方图如图1所示,统计各年龄组的“亚健康族”(日平均睡眠时间符合健康标准的称为“健康族”否则称为“亚健康族”)人数及相应频率,得到统计表如图所示 | 组数 | 分组 | 亚健康族的人数 | 占本组的频率 |
| 第一组 | [10,20) | 100 | 0.5 |
| 第二组 | [20,30) | 195 | P |
| 第三组 | [30,40) | 120 | 0.6 |
| 第四组 | [40,50) | a | 0.4 |
| 第五组 | [50,60) | 30 | 0.3 |
| 第六组 | [60,70] | 15 | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com