
分析 (1)求出解析式,讨论x≥2时,x<2时,去掉绝对值,由二次函数的单调性,即可得到所求减区间;
(2)求出f(x)的分段函数形式,讨论对称轴和区间的关系,根据函数的最值,结合分段函数解方程,即可得到结论.
解答 解:(1)当a=2时,f(x)=x|x-2|,
当x≥2时,f(x)=x2-2x=(x-1)2-1,
当x<2时,f(x)=2x-x2=-(x-1)2+1.
即有f(x)的单调减区间为(1,2);
(2)f(x)=x|x-a|=$\left\{\begin{array}{l}{{x}^{2}-ax,x≥a}\\{ax-{x}^{2},x<a}\end{array}\right.$,
①若a≤0,则f(x)max=f(1)=1-a=$\frac{{a}^{2}}{4}$,
⇒a=-2-2$\sqrt{2}$;
②若a>0,则
(i)$\frac{a}{2}$>1⇒f(x)max=f(1)=$\frac{{a}^{2}}{4}$⇒a∈∅;
(ii) $\frac{a}{2}$≤1≤$\frac{1+\sqrt{2}}{2}$a⇒f(x)max=f( $\frac{a}{2}$)=$\frac{{a}^{2}}{4}$
⇒a∈[2$\sqrt{2}$-2,2];
(iii)1>$\frac{1+\sqrt{2}}{2}$a⇒f(x)max=f(1)=$\frac{{a}^{2}}{4}$⇒a∈∅.
综上:a∈[2$\sqrt{2}$-2,2]∪{-2$\sqrt{2}$-2}.
点评 本题主要考查函数单调性的判断以及函数最值的应用,利用分段函数结合二次函数的图象和性质是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
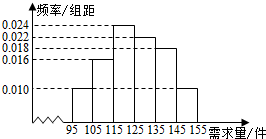 某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.
某商场经销某一种电器商品,在一个销售季度内,每售出一件该商品获利200元,未售出的商品,每件亏损100元,根据以往资料,得到销售季度内市场需求量的频率分布直方图,如图所示,现在经销商为下一个销售季度购进了125件该种电器,以n(单位:件;95≤n≤155)表示下一个销售季度市场需求量,Y(单位:元)表示下一个销售季度内销售 该电器的利润.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com