
分析 直接利用函数的单调性的定义,证明即可.
解答 证明:任取x2>x1>1,函数值作差得
$\begin{array}{l}f({x_1})-f({x_2})=(x_1^2+\frac{2}{x_1})-(x_2^2+\frac{2}{x_2})=(x_1^2-x_2^2)+(\frac{2}{x_1}-\frac{2}{x_2})\\=({x_1}+{x_2})({x_1}-{x_2})+\frac{{2({x_2}-{x_1})}}{{{x_1}{x_2}}}=({x_1}-{x_2})\frac{{{x_1}{x_2}({x_1}+{x_2})-2}}{{{x_1}{x_2}}}\end{array}$
因为x1<x2,所以x1-x2<0,而x1x2>1>0,x1+x2>2,
所以x1x2(x1+x2)-2>0,于是f(x1)-f(x2)<0,即f(x1)<f(x2),
所以函数$f(x)={x^2}+\frac{2}{x}$在数集{x∈R|x>1}上是增加的.
点评 本题考查函数的单调性的证明,考查计算能力.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
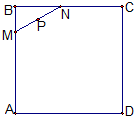 正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )
正方形ABCD的边长为2,(如图),线段MN=1,当点M、N在正方形ABCD的边上滑动一周(保持MN的长度不变)时,线段MN的中点P的轨迹围成一个封闭图形E,现向正方形中随机投入一点,则该点落在E内的概率是( )| A. | $\frac{7}{8}$ | B. | $\frac{π}{16}$ | C. | $1-\frac{π}{16}$ | D. | $\frac{3}{4}+\frac{π}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1,-1) | B. | (0,-1,6) | C. | (0,1,-6) | D. | (0,1,6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com