
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 3 |
科目:高中数学 来源: 题型:选择题
| A. | 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43 | |
| B. | 观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,可得偶函数的导函数为奇函数 | |
| C. | 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8 | |
| D. | 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},2})$ | B. | $({\frac{1}{2},1})∪({1,2})$ | C. | (1,2) | D. | $({\frac{1}{2},∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对于命题p:?x∈R,x2+x+1>0,则¬p:?x∈R,x2+x+1≤0 | |
| B. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| C. | “sinθ=$\frac{1}{2}$”是“θ=30°”的充分不必要条件 | |
| D. | 命题“若x2-3x+2=0,则x=1”的逆否命题是“若x≠1,则x2-3x+2≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
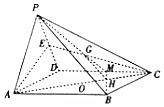 如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.
如图,P是平行四边形ABCD所在平面外一点,E是PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com