练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．下面四个推理中，属于演绎推理的是（　　）
    A．观察下列各式：72=49，73=343，74=2401，…，则72015的末两位数字为43
    B．观察（x2）′=2x，（x4）′=4x3，（cosx）′=-sinx，可得偶函数的导函数为奇函数
    C．在平面上，若两个正三角形的边长比为1：2，则它们的面积比为1：4，类似的，在空间中，若两个正四面体的棱长比为1：2，则它们的体积之比为1：8
    D．已知碱金属都能与水发生还原反应，钠为碱金属，所以钠能与水发生反应

    分析 分别判断各选项，即可得出结论．

    解答 解：选项A、B都是归纳推理，选项C为类比推理，选项D为演绎推理．
    故选D．

    点评 本题考查的是演绎推理的定义，判断一个推理过程是否是演绎推理关键是看他是否符合演绎推理的定义，能否从推理过程中找出“三段论”的三个组成部分．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

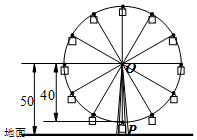    3．如图，某公园摩天轮的半径为40m，点O距地面的高度为50m，摩天轮做匀速转动，每3min转一圈，摩天轮上的点P的起始位置在最低点处．
    （Ⅰ）已知在时刻t（min）时点P距离地面的高度f（t）=Asin（ωt+φ）+h，求2018min时点P距离地面的高度；
    （Ⅱ）当离地面50+20$\sqrt{3}$m以上时，可以看到公园的全貌，求转一圈中有多少时间可以看到公园全貌？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在数列{an}中，a1=1，a2=2，an+2-an=1+（-1）n（n∈N*），则S100=2600．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．函数f（x）=lnx+$\frac{1}{2}$x2+ax（a∈R），g（x）=ex+$\frac{3}{2}$x2
    （1）讨论f（x）的极值点的个数；
    （2）若对于?x＞0，总有f（x）≤g（x），求实数a的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．两个复数z1=a1+b1i，z2=a2+b2i，（a1，b1，a2，b2都是实数且z1≠0，z2≠0），对应的向量在同一直线上的充要条件是（　　）
    A．$\frac{b_1}{a_1}•\frac{b_2}{a_2}=-1$B．a1a2+b1b2=0
    C．$\frac{b_1}{a_1}=\frac{b_2}{a_2}$D．a1b2=a2b1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．lg$\frac{5}{2}$+2lg2-（$\frac{1}{2}$）-1=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数$y=sin\frac{x}{2}+\sqrt{3}cos\frac{x}{2}，x∈R$．的最大值为（　　）
    A．1+$\sqrt{3}$B．2C．1D．$\sqrt{3}+\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知an=$\frac{n-\sqrt{2017}}{n-\sqrt{2016}}$  （ n∈N*），则在数列{an}的前100项中最小项和最大项分别是（　　）
    A．a1，a100B．a100，a44C．a45，a44D．a44，a45

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知a，b，c分别是△ABC内角A，B，C的对边，sin2B=2sinAsinC．若B=90°，且$a=\sqrt{3}$，则△ABC的面积为（　　）
    A．1B．$\frac{3}{2}$C．$\frac{{\sqrt{3}}}{2}$D．3

    查看答案和解析>>

    同步练习册答案