
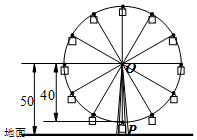
 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.分析 (Ⅰ)由题意求出A、h和ω的值,结合f(0)=10求得φ的值,
写出函数f(x)的解析式,计算t=2018时点P距离地面的高度即可;
(Ⅱ)化简f(t),由f(t)>50+20$\sqrt{3}$求出t的取值范围,
再由t的区间端点值的差求得一圈中可以看到公园全貌的时间.
解答 解:(Ⅰ)依题意,A=40,h=50,T=3,
∴ω=$\frac{2π}{T}$=$\frac{2π}{3}$;
又f(0)=10,
∴φ=-$\frac{π}{2}$;
∴f(t)=40sin($\frac{2π}{3}$t-$\frac{π}{2}$)+50(t≥0);
∴f(2018)=40sin($\frac{2π}{3}$×2018-$\frac{π}{2}$)+50=40sin$\frac{5π}{6}$+50=70,
即第2018min时点P所在位置的高度为70m;
(Ⅱ)由(1)知,f(t)=40sin($\frac{2π}{3}$t-$\frac{π}{2}$)+50=50-40cos($\frac{2π}{3}$t)(t≥0);
依题意:f(t)>50+20$\sqrt{3}$,
∴-40cos($\frac{2π}{3}$t)>20$\sqrt{3}$,
∴cos($\frac{2π}{3}$t)<-$\frac{\sqrt{3}}{2}$,
解得2kπ+$\frac{5π}{6}$<$\frac{2π}{3}$t<2kπ+$\frac{7π}{6}$,k∈N,
即3k+$\frac{5}{4}$<t<3k+$\frac{7}{4}$,k∈N;
∵(3k+$\frac{7}{4}$)-(3k+$\frac{5}{4}$)=$\frac{1}{2}$,
∴转一圈中有0.5min时间可以看到公园全貌.
点评 本题考查了y=Asin(ωx+φ)型函数解析式的求法与三角不等式的解法问题,是综合题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不大于2 | B. | 都小于2 | ||
| C. | 至少有一个不小于2 | D. | 都大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{5n-4}{2}$ | B. | ${a_n}=\frac{3n-2}{2}$ | C. | ${a_n}=\frac{6n-5}{2}$ | D. | ${a_n}=\frac{10n-9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{12}$ | B. | $\frac{5}{12}$ | C. | -$\frac{12}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43 | |
| B. | 观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,可得偶函数的导函数为奇函数 | |
| C. | 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8 | |
| D. | 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com