
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{3}{4}$ |
分析 找出圆心坐标和圆的半径,由直线被圆截取的弦长为2$\sqrt{3}$,可得圆心到直线的距离$\frac{2}{\sqrt{4{a}^{2}+{b}^{2}}}$=1,再利用配方法,即可求出结论.
解答 解:圆的圆心坐标为(0,0),半径r=2,
由直线被圆截取的弦长为2$\sqrt{3}$,可得圆心到直线的距离$\frac{2}{\sqrt{4{a}^{2}+{b}^{2}}}$=1,
∴4a2+b2=4,
t=a$\sqrt{1+2{b}^{2}}$=$\sqrt{{a}^{2}(9-8{a}^{2})}$=$\sqrt{-8({a}^{2}-\frac{9}{16})^{2}+\frac{81}{32}}$,
则a=$\frac{3}{4}$时,t=a$\sqrt{1+2{b}^{2}}$取得最大值.
故选D.
点评 此题考查了直线与圆相交的性质,以及配方法的运用,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | y=log2x | B. | $y=\frac{1}{x}$ | C. | y=2x | D. | $y={x^{\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
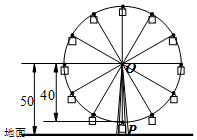 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com