
| A. | y=log2x | B. | $y=\frac{1}{x}$ | C. | y=2x | D. | $y={x^{\frac{2}{3}}}$ |
分析 根据题意,依次分析选项:对于A、由对数函数的性质分析可得其在区间(0,+∞)上为增函数,对于B、由反比例函数的性质分析可得其在区间(0,+∞)上为减函数,对于C、由指数函数的性质分析可得其在区间(0,+∞)上为增函数,对于D、由幂函数的性质分析可得其在区间(0,+∞)上为增函数,综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、函数y=log2x为对数函数,底数a=2>1,在区间(0,+∞)上为增函数,不合题意;
对于B、函数y=$\frac{1}{x}$为反比例函数,在区间(0,+∞)上为减函数,符合题意;
对于C、函数y=2x为指数函数,底数a=2>1,在区间(0,+∞)上为增函数,不合题意;
对于D、函数y=${x}^{\frac{2}{3}}$为幂函数,指数α=$\frac{2}{3}$>0,在区间(0,+∞)上为增函数,不合题意;
故选:B.
点评 本题考查函数的单调性的判断,关键是熟悉常见函数的单调性.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
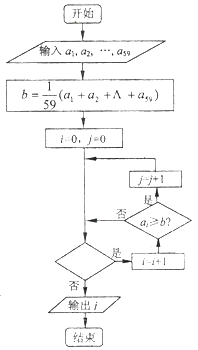 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
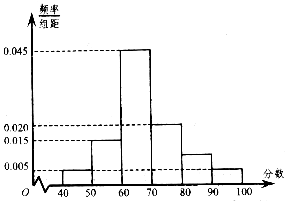 上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.
上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com