
分析 本题利用几何概型求解.欲求恰好落在阴影范围内的概率,只须求出阴影范围内的面积与正方形的面积比即可.为了求出阴影部分的面积,联立由曲线y=x3和曲线y=$\sqrt{x}$两个解析式求出交点坐标,然后在x∈(0,1)区间上利用定积分的方法求出围成的面积即可.
解答 解:联立得$\left\{\begin{array}{l}{y={x}^{3}}\\{y={x}^{\frac{1}{2}}}\end{array}\right.$,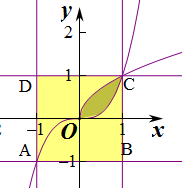
解得 $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$,
设曲线与曲线围成的面积为S,
则S=∫01($\sqrt{x}$-x3)dx=($\frac{2}{3}$x${\;}^{\frac{3}{2}}$-$\frac{1}{4}$x4)|${\;}_{0}^{1}$═$\frac{2}{3}$-$\frac{1}{4}$=$\frac{5}{12}$,
而Ω={(x,y)||x|≤1,|y|≤1},表示的区域是一个边长为2的正方形,
∴Ω上随机投一点P,则点P落入区域A(阴影部分)中的概率P=$\frac{{S}_{阴影}}{S}$=$\frac{\frac{5}{12}}{2×2}$=$\frac{5}{48}$,
故答案为:$\frac{5}{48}$.
点评 本题主要考查几何概型的概率的计算,根据积分公式求出阴影部分的面积是解决本题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2x | B. | $y=\frac{1}{x}$ | C. | y=2x | D. | $y={x^{\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
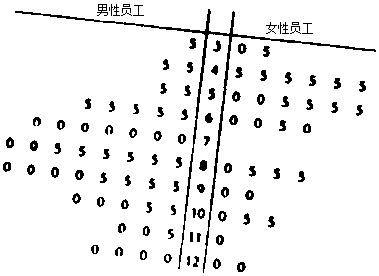
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com