
分析 (Ⅰ)求出函数的导数,计算f′(1)=2,求出切线方程即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间,求出函数的极值即可;
(Ⅲ)得到${({{x_1}+{x_2}})^2}+({{x_1}+{x_2}})$=x1x2-ln(x1x2),令t=x1x2,则φ(t)=t-lnt,根据函数的单调性求出${({{x_1}+{x_2}})^2}+({{x_1}+{x_2}})≥1$,证明结论即可.
解答 解:(Ⅰ)当a=0时,f(x)=lnx+x,则f(1)=1,所以切点为(1,1),
又$f'(x)=\frac{1}{x}+1$,则切线斜率f'(1)=2,
故切线方程为y-1=2(x-1),即2x-y-1=0.
(Ⅱ)g(x)=f(x)-(ax-1)=$lnx-\frac{1}{2}a{x^2}+({1-a})x+1$,
则$g'(x)=\frac{1}{x}-ax+({1-a})$=$\frac{{-a{x^2}+({1-a})x+1}}{x}$,
当a≤0时,∵x>0,∴g'(x)>0.
∴g(x)在(0,+∞)上是递增函数,函数g(x)无极值点,
当a>0时,$g'(x)=\frac{{-a{x^2}+({1-a})x+1}}{x}$=$-\frac{{a({x-\frac{1}{a}})({x+1})}}{x}$,
令g'(x)=0得$x=\frac{1}{a}$,∴当$x∈({0,\frac{1}{a}})$时,g'(x)>0;当$x∈({\frac{1}{a},+∞})$时,g'(x)<0.
因此g(x)在$({0,\frac{1}{a}})$上是增函数,在$({\frac{1}{a},+∞})$上是减函数.
∴$x=\frac{1}{a}$时,g(x)有极大值$g({\frac{1}{a}})=ln\frac{1}{a}-\frac{a}{2}×\frac{1}{a^2}+$$({1-a})×\frac{1}{a}+1=\frac{1}{2a}-lna$.
综上,当a≤0时,函数g(x)无极值;当a>0时,函数g(x)有极大值$\frac{1}{2a}-lna$;
(Ⅲ)证明:当a=-2时,f(x)=lnx+x2+x,x>0,
由f(x1)+f(x2)+x1x2=0,
即$ln{x_1}+x_1^2+{x_1}+ln{x_2}$$+x_2^2+{x_2}+{x_1}{x_2}=0$,
从而${({{x_1}+{x_2}})^2}+({{x_1}+{x_2}})$=x1x2-ln(x1x2),
令t=x1x2,则φ(t)=t-lnt,得φ′(t)=$\frac{t-1}{t}$,
可知φ(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
∴φ(t)≥φ(1)=1,∴${({{x_1}+{x_2}})^2}+({{x_1}+{x_2}})≥1$,
因为x1>0,x2>0∴${x_1}+{x_2}≥\frac{{\sqrt{5}-1}}{2}$.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想,是一道中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
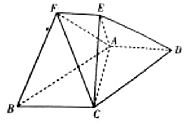 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
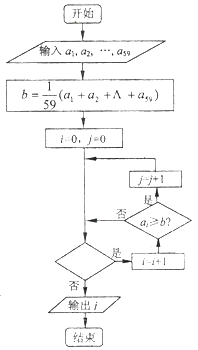 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com