
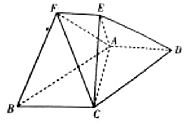
 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.分析 (Ⅰ)证明:EC⊥平面ADE,即可证明平面FCE⊥平面ADE;
(Ⅱ)若直线AE与平面ACF所成的角的正弦值为$\frac{{\sqrt{3}}}{3}$,建立空间直角坐标系,利用向量方法求AD的值.
解答 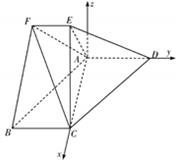 (Ⅰ)证明:因为AD⊥平面AEC,EC?平面AEC,所以AD⊥EC.
(Ⅰ)证明:因为AD⊥平面AEC,EC?平面AEC,所以AD⊥EC.
又$AC=\sqrt{2}$,AE=EC=1,所以AC2=AE2+EC2,所以AE⊥EC.
又AE∩AD=A,所以EC⊥平面ADE.
因为EC?平面FCE,所以平面FCE⊥平面ADE.
(Ⅱ)解:以A为原点,AC,AD所在直线为x,y轴,过点A且垂直于平面ABCD的直线为z轴,建立空间直角坐标系,设AD=2a(a>0),则A(0,0,0),$C({\sqrt{2},0,0})$,$E({\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2}})$,$F({\frac{{\sqrt{2}}}{2},-a,\frac{{\sqrt{2}}}{2}})$,
设平面ACF的一个法向量为$\overrightarrow m=({x,y,z})$,因为$\overrightarrow{AC}=({\sqrt{2},0,0})$,$\overrightarrow{AF}=({\frac{{\sqrt{2}}}{2},-a,\frac{{\sqrt{2}}}{2}})$,
所以$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{AC}=0\\ \overrightarrow m•\overrightarrow{AF}=0\end{array}\right.$即$\left\{\begin{array}{l}\sqrt{2}x=0\\ \frac{{\sqrt{2}}}{2}x-ay+\frac{{\sqrt{2}}}{2}z=0\end{array}\right.$取$z=\sqrt{2}$,得$y=\frac{1}{a}$,则$\overrightarrow m=({0,\frac{1}{a},\sqrt{2}})$.
又因为$\overrightarrow{AE}=({\frac{{\sqrt{2}}}{2},0,\frac{{\sqrt{2}}}{2}})$,设直线AE与平面ACF所成的角为θ,则$sinθ=\frac{{|{\overrightarrow{AE}•\overrightarrow m}|}}{{|{\overrightarrow{AE}}||{\overrightarrow m}|}}$=$\frac{1}{{\sqrt{\frac{1}{a^2}+2}}}=\frac{{\sqrt{3}}}{3}$,
解得a=1(a=-1舍去),故AD=2.
点评 本题考查直线与平面垂直、平面与平面垂直的证明,考查直线AE与平面ACF所成的角的求法,考查向量方法的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
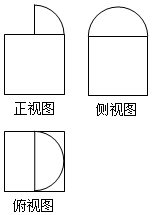 一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )
一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )| A. | $8+\frac{π}{3}$ | B. | $8+\frac{π}{4}$ | C. | $8+\frac{4π}{3}$ | D. | $4+\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
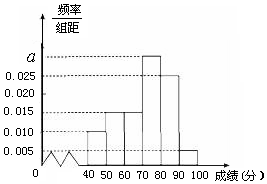 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{a^2}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{b^2}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x}$ | B. | $f(x)=\frac{x}{2}$ | C. | f(x)=log2x | D. | f(x)=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
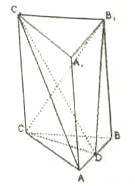 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com