
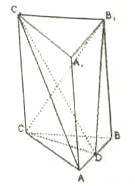
 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.分析 (1)推导出CC1⊥AB,CD⊥AB,从而AB⊥平面C1CD,由此能证明平面C1CD⊥平面ADC1.
(2)连结BC1,交B1C于点O,连结DO.则DO∥AC1,由此能证明AC1∥平面CDB1.
(3)三棱锥D-CAB1的体积${V}_{D-CA{B}_{1}}={V}_{{B}_{1}-CBD}$,由此能求出结果.
解答 证明:(1)∵CC1⊥平面ABC,又AB?平面ABC,∴CC1⊥AB,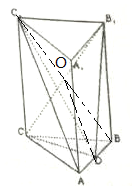
∵△ABC是等边三角形,CD为AB边上的中线,
∴CD⊥AB,(2分)
∵CD∩CC1=C,∴AB⊥平面C1CD,
∵AB?平面ADC1,
∴平面C1CD⊥平面ADC1.
(2)连结BC1,交B1C于点O,连结DO.
则O是BC1的中点,DO是△BAC1的中位线.
∴DO∥AC1.
∵DO?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1.(8分)
解:(3)∵CC1⊥平面ABC,BB1∥CC1,
∴BB1⊥平面ABC.
∴BB1 为三棱锥D-CBB1 的高.
∴三棱锥D-CAB1的体积:
${V}_{D-CA{B}_{1}}={V}_{{B}_{1}-CBD}$=$\frac{1}{3}{S}_{△BCD}•B{B}_{1}$=$\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{3}}{4}×{4}^{2}×8$=$\frac{16\sqrt{3}}{3}$.
∴三棱锥D-CAB1的体积为$\frac{16\sqrt{3}}{3}$.…(12分)
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
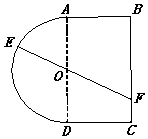 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
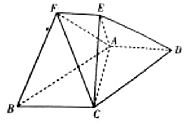 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
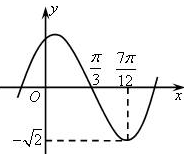 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
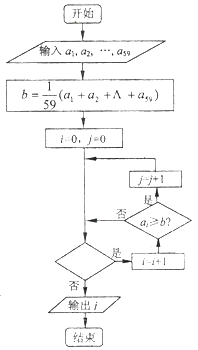 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com