
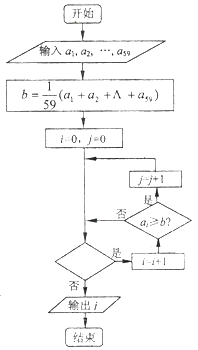
 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,由程序框图知:要想判断所有59位学生的成绩ai≥b(i=1,2,3,…59)是否成立,判断框中应填入的条件是i≤58?
解答 解:由程序框图知:
先输入59位同学的数学成绩,并求出平均分b,
然后依次判断59名学生的成绩ai≥b(i=1,2,3,…59)是否成立,
若成立,j=j+1,再判断下一位,若不成立,直接判断下一位,
由此得到要想判断所有59位学生的成绩ai≥b(i=1,2,3,…59)是否成立,
判断框中应填入的条件是i≤58?
故选:B.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{a^2}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{b^2}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
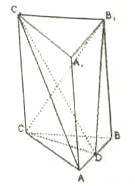 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=log2x | B. | $y=\frac{1}{x}$ | C. | y=2x | D. | $y={x^{\frac{2}{3}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
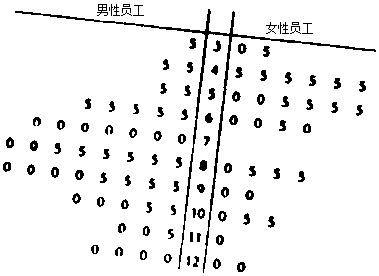
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com