
分析 (1)已知等式利用正弦定理化简,根据sinB不为0确定出tanA的值,进而求出cosA的值;
(2)由cosA的值,利用同角三角函数间的基本关系求出sinA的值,再利用正弦定理求出sinB的值,进而求出cosB的值,确定出sinA=cosB,cosA=sinB,即C为直角,确定出三角形面积即可.
解答 解:(1)在△ABC中,内角A、B、C的对边分别为a,b,c,
将等式2asinB-$\sqrt{5}$bcosA=0,利用正弦定理化简得:2sinAsinB-$\sqrt{5}$sinBcosA=0,
∵sinB≠0,∴2sinA-$\sqrt{5}$cosA=0,即tanA=$\frac{\sqrt{5}}{2}$,
则cosA=$\sqrt{\frac{1}{1+ta{n}^{2}A}}$=$\frac{2}{3}$;
(2)∵cosA=$\frac{2}{3}$,∴sinA=$\frac{\sqrt{5}}{3}$,
∵a=$\sqrt{5}$,b=2,
∴由正弦定理得:sinB=$\frac{bsinA}{a}$=$\frac{2}{3}$,cosB=$\frac{\sqrt{5}}{3}$,
∴sinA=cosB,cosA=sinB,即A+B=C=$\frac{π}{2}$,
则S△ABC=$\frac{1}{2}$×$\sqrt{5}$×2=$\sqrt{5}$.
点评 此题考查了正弦、余弦定理,同角三角函数间的基本关系,熟练掌握定理及公式是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | [-5,-3] | B. | [-6,-$\frac{9}{8}$] | C. | [-6,-2] | D. | [-4,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
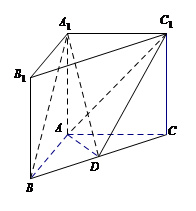 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
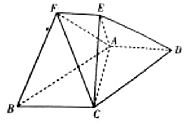 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
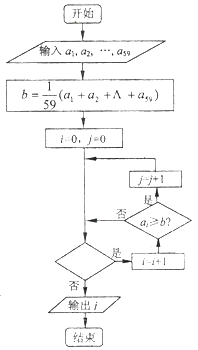 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com