
| A. | [-5,-3] | B. | [-6,-$\frac{9}{8}$] | C. | [-6,-2] | D. | [-4,-3] |
分析 分x=0,0<x≤1,-2≤x<0三种情况进行讨论,分离出参数a后转化为函数求最值即可,利用导数即可求得函数最值,注意最后要对a取交集.
解答 解:当x=0时,不等式ax3-x2+4x+3≥0对任意a∈R恒成立;
当0<x≤1时,ax3-x2+4x+3≥0可化为a≥$\frac{1}{x}$-$\frac{4}{{x}^{2}}$-$\frac{3}{{x}^{3}}$,
令f(x)=$\frac{1}{x}$-$\frac{4}{{x}^{2}}$-$\frac{3}{{x}^{3}}$,
则f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{8}{{x}^{3}}$+$\frac{9}{{x}^{4}}$=-$\frac{(x-9)(x+1)}{{x}^{4}}$(*),
当0<x≤1时,f′(x)>0,f(x)在(0,1]上单调递增,
f(x)max=f(1)=-6,∴a≥-6;
当-2≤x<0时,ax3-x2+4x+3≥0可化为a≤$\frac{1}{x}$-$\frac{4}{{x}^{2}}$-$\frac{3}{{x}^{3}}$,
由(*)式可知,当-2≤x<-1时,f′(x)<0,f(x)单调递减,当-1<x<0时,f′(x)>0,f(x)单调递增,
f(x)min=f(-1)=-2,∴a≤-2;
综上所述,实数a的取值范围是-6≤a≤-2,即实数a的取值范围是[-6,-2].
故选:C.
点评 本题考查利用导数研究函数的最值,考查转化思想、分类与整合思想,按照自变量讨论,最后要对参数范围取交集.若按照参数讨论则取并集,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 若0<α<$\frac{π}{2}$,则sin α<tan α | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限角或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)且k≠0,则sin α=$\frac{4}{5}$ | |
| D. | 若α=-$\frac{π}{3}$,则cos α=$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120种 | B. | 175种 | C. | 220种 | D. | 820种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2018}+1$ | B. | $\sqrt{2018}-1$ | C. | $\sqrt{2017}-1$ | D. | $\sqrt{2017}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
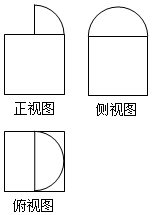 一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )
一个机器零件的三视图如图所示,其中侧视图是一个半圆与边长为2的正方形,俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为( )| A. | $8+\frac{π}{3}$ | B. | $8+\frac{π}{4}$ | C. | $8+\frac{4π}{3}$ | D. | $4+\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com