
分析 (1)由周期公式可得ω,ω>0,再由对称中心可得φ值,可得f(x)解析式,由函数图象变换和诱导公式化简可得;
(2)根据x的范围,求出sinx0+cos2x0=1,继而求出sinx0的值,即可判断,
(3)根据函数零点存在定理可得cos2x+asinx=0,再分类讨论即可求出答案
解答 解:(1)∵函数f(x)=sin(ωx+φ)的周期为π,ω>0,∴ω=$\frac{2π}{T}$=2,
又曲线y=f(x)的一个对称中心为($\frac{π}{4}$,0),φ∈(0,π),
∴sin(2×$\frac{π}{4}$+φ)=0,可得φ=$\frac{π}{2}$,
∴f(x)=cos2x,
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,
再将y=cosx的图象向右平移$\frac{π}{2}$个单位长度后得到函数g(x)=cos(x-$\frac{π}{2}$)的图象,
由诱导公式化简可得g(x)=sinx;
(2)当x∈($\frac{π}{6}$,$\frac{π}{4}$),$\frac{1}{2}$<sinx<$\frac{\sqrt{2}}{2}$,0<cos2x<$\frac{1}{2}$,
∵f($\frac{π}{6}$)=$\frac{1}{2}$,则g(x0)>f($\frac{π}{6}$)>f(x0),
∴g(x0)+f(x0)=2f($\frac{π}{6}$),
即sinx0+cos2x0=1,
化简得sinx0=0或sinx0=$\frac{1}{2}$与$\frac{1}{2}$<sinx0<$\frac{\sqrt{2}}{2}$矛盾,
所以不存在x0∈($\frac{π}{6}$,$\frac{π}{4}$),使得f(x0),g(x0),f($\frac{π}{6}$)按照某种顺序成等差数列.
(3)F(x)=f(x)+ag(x)=0,
即cos2x+asinx=0,
当sinx=0,显然不成立,
当sinx≠0时,a=-$\frac{cos2x}{sinx}$=2sinx-$\frac{1}{sinx}$,令t=sinx,则当x∈[0,2π]时,t∈[-1,1],
由函数a=2t-$\frac{1}{t}$,t∈[-1,1],以及t=sinx,x∈[0,2π]的图象可知,
当a=±1时,a=2sinx-$\frac{1}{sinx}$在[0,2π]内恰有3个零点.
综上所述,a=±1
点评 本题考查同角三角函数基本关系,三角恒等变换,三角函数的图象与性质,考查函数、函数的导数、函数的零点等基础知识,考查运算求解能力,抽象概括能力,推理论证能力,考查函数与方程思想、数形结合思想、分类与整合思想、化归与转化思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9] |
| 女生人数 | 2 | 4 | 8 | 4 | 2 |
| 男生人数 | 1 | 5 | 6 | 5 | 3 |
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | 12 | 8 | 20 |
| 女生 | 14 | 6 | 20 |
| 合计 | 26 | 14 | 40 |
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-5,-3] | B. | [-6,-$\frac{9}{8}$] | C. | [-6,-2] | D. | [-4,-3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
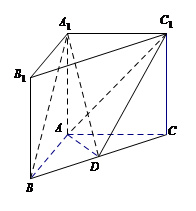 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
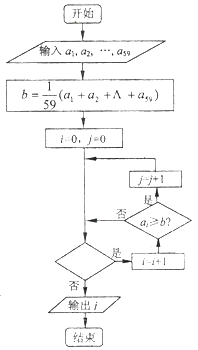 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com