
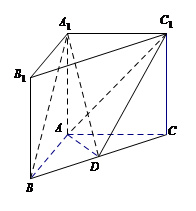
 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.分析 (Ⅰ)根据线面垂直的判定定理进行证明即可,
(Ⅱ)根据线面平行的判定定理进行证明即可.
(III)根据二面角的定义或者建立空间坐标系,求出平面的法向量,利用向量法进行求解即可.
解答 解:(I)因AB=AC,D为BC中点,故AD⊥BC(1分).
又因在直三棱柱A1B1C1-ABC中,CC1⊥平面ABC,故AD⊥CC1(2分).
又BC∩CC1=C(3分),
故AD⊥平面BCC1B1(4分).
用向量方法证明本题请对应给分.
本题可分别以AB,AC,AA1为x,y,z轴建立空间直角坐标系,
也可分别以DC,DA,AD1(D1为棱B1C1中点)为x,y,z轴建立空间直角坐标系.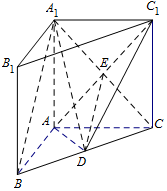
(II)如图,连接A1C∩AC1=E,连接DE.因D、E分别是BC、A1C的中点,故DE是△A1BC的中位线(5分),
故A1B∥DE(6分).因A1B?平面ADC1(7分),
故A1B∥平面ADC1(8分).
用向量方法证明本题请如下给分:求出平面ADC1的法向量(2分),
因A1B?平面ADC1(7分),
故A1B∥平面ADC1(8分).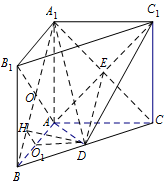
(III)解法一:连接B1A∩BA1=O,分别取OB、AB中点H、O1,连接DH、DO1.
因为四边形ABB1A1是正方形且O1,H分别是BA,BO中点,故HO1⊥AB.
又因O1,H分别是BA,BC中点且AB⊥AC,故O1D⊥AB,
故∠O1HD就是二面角A-A1B-D的平面角(10分).
设AB=2,则在Rt△HO1D中,∠HO1D=90°且${O_1}D=\frac{1}{2}AC=1,{O_1}H=\frac{1}{2}OA=\frac{{\sqrt{2}}}{2}$,
故$HD=\frac{{\sqrt{6}}}{2}$,故$cos∠{O_1}HD=\frac{{{O_1}H}}{DH}=\frac{{\sqrt{3}}}{3}$(12分).
解法二:设AB=AC=2,则$BC=2\sqrt{2}$,故AB2+AC2=BC2,故AB⊥AC(9分),
又因三棱柱A1B1C1-ABC为直三棱柱,故AB,AC,AA1两两垂直,故可建系如图.
则平面AA1B的法向量为$\overrightarrow{n_1}=(0,1,0)$(10分).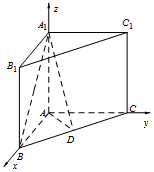
又$\overrightarrow{{A_1}B}=(2,0,-2),\overrightarrow{{A_1}D}=(1,1,-2)$,
设平面A1BD的法向量$\overrightarrow{n_2}=(x,y,z)$,
则$\left\{\begin{array}{l}x-z=0\\ x+y-2z=0\end{array}\right.$.
令z=1可得$\overrightarrow{n_2}=(1,1,1)$(11分).
设所求二面角为θ,由图可知θ为锐角,故$cosθ=\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{{\sqrt{3}}}{3}$(12分).
点评 本题主要考查空间线面平行和线面垂直的判定以及空间二面角的求解,利用定义法或者建立坐标系,利用向量法是解决本题的关键.考查学生的运算和推理能力.


科目:高中数学 来源: 题型:选择题
| A. | 120种 | B. | 175种 | C. | 220种 | D. | 820种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
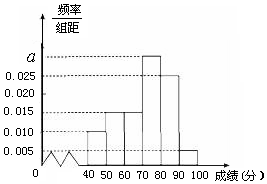 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{a^2}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{b^2}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
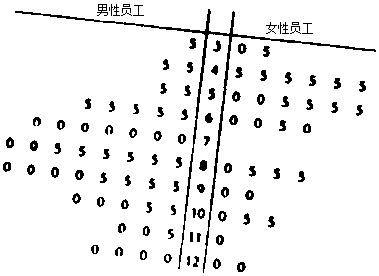
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com