
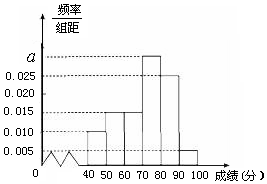
 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:分析 (1)根据条形统计图求出a的值,确定出优生率,找出众数,平均值即可;
(2)根据题意得出所有等可能的情况数,找出“最佳组合”数,即可确定出选出的两组为“最佳组合”的概率.
解答 解:(1)根据题意得:a=0.1-(0.005+0.010+0.015×2+0.025)=0.03,
成估计这次考试中该学科的众数75分;
平均数为45×0.1+55×0.15+65×0.15+75×0.3+85×0.25+95×0.05=71;
(2)所有的组合数:(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),
即n=5+4+3+2+1=15,
符合“最佳组合”条件的有:(1,4),(1,5),(1,6),(2,5),(2,6),(3,6),
即m=6,
则P=$\frac{m}{n}$=$\frac{6}{15}$=$\frac{2}{5}$.
点评 此题考查了列举法计算基本事件数及事件发生的概率,众数,平均数,弄清统计图中的数据是解本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
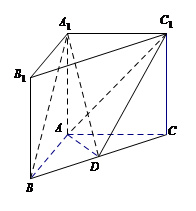 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
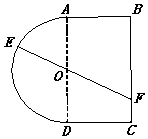 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
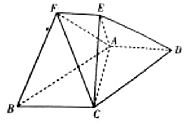 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com