
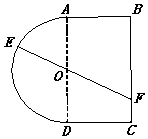
 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.分析 (1)通过过点O作OG⊥BC于G,利用OG=1、$OF=\frac{OG}{sinθ}=\frac{1}{sinθ}$、$EF=1+\frac{1}{sinθ}$、弧AE=θ及时间、路程与速度之间的关系即得结论;
(2)通过(1)求导,利用函数的单调性即得结论.
解答  解:(1)过O作OG⊥BC于G,则OG=1,$OF=\frac{OG}{sinθ}=\frac{1}{sinθ}$,$EF=1+\frac{1}{sinθ}$,
解:(1)过O作OG⊥BC于G,则OG=1,$OF=\frac{OG}{sinθ}=\frac{1}{sinθ}$,$EF=1+\frac{1}{sinθ}$,
弧AE=θ,
所以$T(θ)=\frac{弧AE}{5v}+\frac{EF}{6v}=\frac{θ}{5v}+\frac{1}{6vsinθ}+\frac{1}{6v}$,$θ∈[\frac{π}{4},\frac{3π}{4}]$.…(7分)
(2)$T(θ)=\frac{θ}{5v}+\frac{1}{6vsinθ}+\frac{1}{6v}$,$T'(θ)=\frac{1}{5v}-\frac{cosθ}{{6v{{sin}^2}θ}}=\frac{{6{{sin}^2}θ-5cosθ}}{{30v{{sin}^2}θ}}=-\frac{(2cosθ+3)(3cosθ-2)}{{30v{{sin}^2}θ}}$,…(10分)
记$cos{θ_0}=\frac{2}{3}$,${θ_0}∈[\frac{π}{4},\frac{3π}{4}]$,
| θ | $(\frac{π}{4},{θ_0})$ | θ0 | $({θ_0},\frac{3π}{4})$ |
| T'(θ) | - | 0 | + |
| T(θ) | 减 | 增 |
点评 本题考查根据实际问题选择函数类型,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
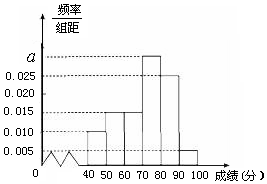 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$ | B. | $\frac{a^2}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{b^2}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x}$ | B. | $f(x)=\frac{x}{2}$ | C. | f(x)=log2x | D. | f(x)=2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
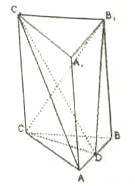 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com