
分析 化简函数f(x),令sinx=t,t∈[0,1],求出f(t)在t∈[0,1]的最大值函数g(a),再令g(a)=0,求对应a的值是否存在即可.
解答 解:∵y=cos2x+asinx+$\frac{5a}{8}$-$\frac{5}{2}$=-sin2x+asinx+$\frac{5a}{8}$-$\frac{3}{2}$,
令sinx=t,t∈[0,1],
∴f(t)=-t2+at+$\frac{5a}{8}$-$\frac{3}{2}$,对称轴为t=$\frac{1}{2}$a,
①当a≤0时,函数f(t)在[0,1]上是减函数,
∴f(t)的最大值是g(a)=f(0)=$\frac{5a}{8}$-$\frac{3}{2}$=0,解得a=$\frac{12}{5}$,不符合题意,
②当a≥2时,函数f(t)在[0,1]上是增函数,
∴f(x)的最大值是g(a)=f(1)=$\frac{13a}{8}$-$\frac{5}{2}$=0,解得a=$\frac{20}{13}$,不符合题意,
③当0<a<2时,f(x)在x∈[0,1]的最大值是g($\frac{1}{2}$a)=f($\frac{1}{2}$a)=$\frac{{a}^{2}}{4}$+$\frac{5a}{8}$-$\frac{3}{2}$=0,
解得a=-4(舍去),或a=$\frac{3}{2}$.
综上,存在a=$\frac{3}{2}$时,函数在闭区间[0,π]上的最大值是0.
点评 本题考查了二次函数的性质与应用问题,也考查了分类讨论的数学思想,其中求出最大值函数 g(a)是解题的关键,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:选择题
| A. | {-$\frac{4}{3}$,$\frac{2}{3}$} | B. | {$\frac{4}{3}$,-$\frac{2}{3}$} | C. | {-$\frac{4}{3}$,$\frac{2}{3}$,$\frac{4}{3}$} | D. | {-$\frac{4}{3}$,-$\frac{2}{3}$,$\frac{2}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
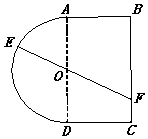 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
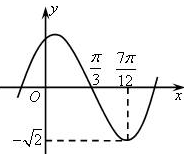 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com