
分析 (1)求出f(x)的导数,可得切线的斜率,由直线垂直的条件:斜率之积为-1,解方程可得a的值;
(2)求出f(x)的导数,讨论当a≤0时,当a>0时,由导数大于0,可得增区间;导数小于0,可得减区间,注意定义域;
(3)对a讨论,当a<0时,当a=0时,当a>0时,判断f(x)的单调性,结合零点存在定理,即可判断零点个数.
解答 解:(1)由题可知f(x)的定义域为(0,+∞),
因为$f(x)=lnx-\frac{1}{2}a{x^2}$,所以$f'(x)=\frac{1}{x}-ax$=$\frac{{1-a{x^2}}}{x}$,
可得切线的斜率为$\frac{1-4a}{2}$,
又因为切线与直线2x+y+2=0垂直,
直线2x+y+2=0的斜率为-2,
可得(-2)×$\frac{1-4a}{2}$=-1,解得a=0;
(2)由(1)知:$f'(x)=\frac{1}{x}-ax$=$\frac{{1-a{x^2}}}{x}$,x>0,
当a≤0时,f'(x)>0,所以f(x)在(0,+∞)上单调递增;
当a>0时,由f'(x)>0得$x<\sqrt{\frac{1}{a}}$,由f'(x)<0得$x>\sqrt{\frac{1}{a}}$,
所以f(x)在$({0,\sqrt{\frac{1}{a}}})$上单调递增,在$({\sqrt{\frac{1}{a}},+∞})$上单调递减.
综上所述:当a≤0时,f(x)在(0,+∞)上单调递增;
当a>0时,f(x)在$({0,\sqrt{\frac{1}{a}}})$上单调递增,在$({\sqrt{\frac{1}{a}},+∞})$上单调递减;
(3)由(2)可知,
当a<0时,f(x)在[1,e2]上单调递增,
而f(1)=-$\frac{1}{2}$a>0,故f(x)在[1,e2]上没有零点;
当a=0时,f(x)在[1,e2]上单调递增,
而f(1)=-$\frac{1}{2}$a=0,故f(x)在[1,e2]上有一个零点;
当a>0时,①若$\sqrt{\frac{1}{a}}≤1$,即a≥1时,f(x)在[1,e2]上单调递减,
∵$f(1)=-\frac{1}{2}a<0$,∴f(x)在[1,e2]上没有零点;
②若$1<\sqrt{\frac{1}{a}}≤{e^2}$,即$\frac{1}{e^4}<a<1$时,f(x)在$[{1,\sqrt{\frac{1}{a}}}]$上单调递增,
在$[{\sqrt{\frac{1}{a}},{e^2}}]$上单调递减,而$f(1)=-\frac{1}{2}a<0$,$f({\sqrt{\frac{1}{a}}})=-\frac{1}{2}lna-\frac{1}{2}$,$f({e^2})=2-\frac{1}{2}a{e^4}$,
若$f({\sqrt{\frac{1}{a}}})=-\frac{1}{2}lna-$$\frac{1}{2}<0$,即$a>\frac{1}{e}$时,f(x)在[1,e2]上没有零点;
若$f({\sqrt{\frac{1}{a}}})=-\frac{1}{2}lna-$$\frac{1}{2}=0$,即$a=\frac{1}{e}$时,f(x)在[1,e2]上有一个零点;
若$f({\sqrt{\frac{1}{a}}})=-\frac{1}{2}lna-$$\frac{1}{2}>0$,即$a<\frac{1}{e}$时,由$f({e^2})=2-\frac{1}{2}a{e^4}>0$得$a<\frac{4}{e^4}$,
此时,f(x)在[1,e2]上有一个零点;
由$f({e^2})=2-\frac{1}{2}a{e^4}≤0$得$a≥\frac{4}{e^4}$,此时,f(x)在[1,e2]上有两个零点;
③若$\sqrt{\frac{1}{a}}≥{e^2}$,即$0<a≤\frac{1}{e^4}$时,f(x)在[1,e2]上单调递增,
∵$f(1)=-\frac{1}{2}a<0$,$f({e^2})=2-\frac{1}{2}a{e^4}>0$,∴f(x)在[1,e2]上有一个零点.
综上所述:当$0≤a<\frac{4}{e^4}$或$a=\frac{1}{e}$时,f(x)在[1,e2]上有一个零点;
当a<0或$a>\frac{1}{e}$时,f(x)在[1,e2]上没有零点;
当$\frac{4}{e^4}≤a<\frac{1}{e}$时,f(x)在[1,e2]上有两个零点.
点评 本题考查导数的运用:求切线的斜率和单调区间,同时考查函数的零点个数问题的解法,注意运用导数判断单调性,以及分类讨论的思想方法,正确分类是解题的关键,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
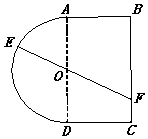 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示.小球从A点出发以5v的速度沿半圆O轨道滚到某点E处后,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F.设∠AOE=θ弧度,小球从A到F所需时间为T.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<k<1 | B. | k>1 | C. | k<-1 | D. | k<-1或k>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com