
分析 (1)由题知$2+\frac{p}{2}=3,\;\;p=2$,即可得到抛物线方程;
(2)设切线方程为:y-y0=k(x-x0),可得切线与x轴的交点为$({{x_0}-\frac{y_0}{k},\;\;0})$,
圆心(2,0)到切线的距离为2,得:$(x_0^2-4{x_0}){k^2}+(4{y_0}-2{x_0}{y_0})k+y_0^2-4=0$.
设两条切线的斜率分别为k1,k2,则${k_1}+{k_2}=\frac{{2{x_0}{y_0}-4{y_0}}}{{x_0^2-4{x_0}}},\;\;{k_1}\;•\;{k_2}=\frac{y_0^2-4}{{x_0^2-4{x_0}}}$,
∴${S_{△PAB}}=\frac{1}{2}|{({{x_0}-\frac{y_0}{k_1}})-({{x_0}-\frac{y_0}{k_2}})}|\;•\;{y_0}=\frac{1}{2}y_0^2|{\frac{{{k_1}-{k_2}}}{{{k_1}{k_2}}}}|=2\frac{x_0^2}{{{x_0}-1}}$=$2\frac{{{{({x_0}-1)}^2}+2({x_0}-1)+1}}{{{x_0}-1}}=2[{({x_0}-1)+\frac{1}{{{x_0}-1}}+2}]$.
根据x0≥5可求得△PAB面积的最小值为$\frac{25}{2}$.
解答 解:( )由题知$2+\frac{p}{2}=3,\;\;p=2$,
所以抛物线方程为:y2=4x. …(4分)
(2)设切线方程为:y-y0=k(x-x0),令y=0,解得$x={x_0}-\frac{y_0}{k}$,
所以切线与x轴的交点为$({{x_0}-\frac{y_0}{k},\;\;0})$,
圆心(2,0)到切线的距离为$d=\frac{{|2k+{y_0}-k{x_0}|}}{{\sqrt{{k^2}+1}}}=2$,
∴${(2k+{y_0}-k{x_0})^2}=4({k^2}+1)$,
整理得:$(x_0^2-4{x_0}){k^2}+(4{y_0}-2{x_0}{y_0})k+y_0^2-4=0$.
设两条切线的斜率分别为k1,k2,
则${k_1}+{k_2}=\frac{{2{x_0}{y_0}-4{y_0}}}{{x_0^2-4{x_0}}},\;\;{k_1}\;•\;{k_2}=\frac{y_0^2-4}{{x_0^2-4{x_0}}}$,
∴${S_{△PAB}}=\frac{1}{2}|{({{x_0}-\frac{y_0}{k_1}})-({{x_0}-\frac{y_0}{k_2}})}|\;•\;{y_0}=\frac{1}{2}y_0^2|{\frac{{{k_1}-{k_2}}}{{{k_1}{k_2}}}}|=2\frac{x_0^2}{{{x_0}-1}}$
=$2\frac{{{{({x_0}-1)}^2}+2({x_0}-1)+1}}{{{x_0}-1}}=2[{({x_0}-1)+\frac{1}{{{x_0}-1}}+2}]$.
记t=x0-1∈[4,+∞),则$f(t)=t+\frac{1}{t}+2$.
∵$f'(t)=1-\frac{1}{t^2}=\frac{{{t^2}-1}}{t^2}>0$,∴f(t)在[4,+∞)上单增,
∴$f(t)≥4+\frac{1}{4}+2=\frac{25}{4}$,∴${S_{△PAB}}≥2×\frac{25}{4}=\frac{25}{2}$,
∴△PAB面积的最小值为$\frac{25}{2}$. …(12分)
点评 本题考查了抛物线的方程,直线与圆的位置关系,三角形的面积最值计算,属于中档题.


科目:高中数学 来源: 题型:解答题
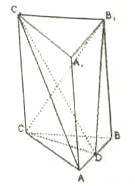 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com