
分析 根据直线和圆相交的条件求出a,b的关系,利用线性规划求出对应区域的面积,结合几何概型的概率公式进行计算即可.
解答 解:根据题意,得$\left\{\begin{array}{l}{-2≤a≤2}\\{-2≤b≤2}\end{array}\right.$,
又直线x+y=1与圆(x-a)2+(y-b)2=2相交,
d≤r,
即$\frac{|a+b-1|}{\sqrt{2}}$≤$\sqrt{2}$,
得|a+b-1|≤2,
所以-1≤a+b≤3;
画出图形,如图所示;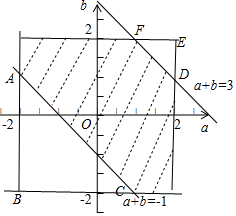
则事件“直线x+y=1与圆(x-a)2+(y-b)2=2相交”发生的概率为
P=$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{{4}^{2}-\frac{1}{2}{×3}^{2}-\frac{1}{2}{×1}^{2}}{{4}^{2}}$=$\frac{11}{16}$.
故答案为:$\frac{11}{16}$
点评 本题主要考查几何概型的计算,根据直线和圆相交的位置关系求出a,b的关系是解决本题的关键.注意利用数形结合以及线性规划的知识.


科目:高中数学 来源: 题型:解答题
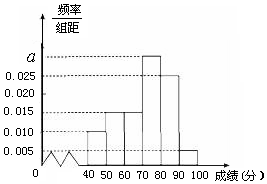 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
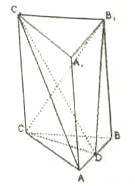 三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.
三棱柱ABC-A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为边AB的中点,且CC1=2AB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
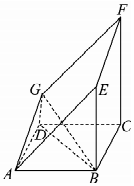 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
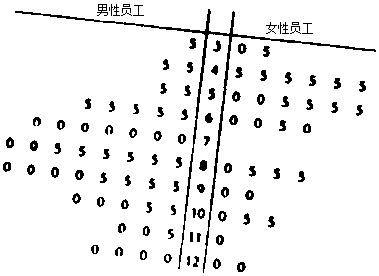
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com