
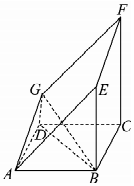
 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.分析 (Ⅰ)证明:AD⊥DB,GD⊥DB,即可证明BD⊥平面ADG;
(Ⅱ)建立空间直角坐标系,利用向量方法求直线GB与平面AEFG所成角的正弦值.
解答 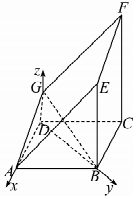 (Ⅰ)证明:在△BAD中,∵AB=2AD=2,∠BAD=60°.
(Ⅰ)证明:在△BAD中,∵AB=2AD=2,∠BAD=60°.
由余弦定理BD2=AD2+AB2-2AB•ADcos60°,$BD=\sqrt{3}$,
∵AB2=AD2+DB2,
∴AD⊥DB,
在直平行六面体中,GD⊥平面ABCD,DB?平面ABCD,∴GD⊥DB,
又AD∩GD=D,
∴BD⊥平面ADG.
(Ⅱ)解:如图以D为原点建立空间直角坐标系D-xyz,
∵∠BAE=∠GAD=45°,AB=2AD=2,
∴A(1,0,0),$B(0,\sqrt{3},0)$,$E(0,\sqrt{3},2)$,G(0,0,1),$\overrightarrow{AE}=(-1,\sqrt{3},2)$,$\overrightarrow{AG}=(-1,0,1)$,$\overrightarrow{GB}=(0,\sqrt{3},-1)$,
设平面AEFG的法向量$\overrightarrow n=(x,y,z)$,$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{AE}=-x+\sqrt{3}y+2z=0\\ \overrightarrow n•\overrightarrow{AG}=-x+z=0\end{array}\right.$令x=1,得$y=\frac{{-\sqrt{3}}}{3}$,z=1,
∴$\overrightarrow n=(1,-\frac{{\sqrt{3}}}{3},1)$,
设直线GB和平面AEFG的夹角为θ,
∴$sinθ=|cos<\overrightarrow{GB},\overrightarrow n>|=|\frac{{\overrightarrow{GB}•\overrightarrow n}}{{|\overrightarrow{GB}|•|\overrightarrow n|}}|=\frac{{\sqrt{21}}}{7}$,
所以直线GB与平面AEFG所成角的正弦值为$\frac{{\sqrt{21}}}{7}$.
点评 本题考查直线与平面垂直,考查直线GB与平面AEFG所成的角的求法,考查向量方法的运用,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
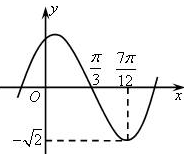 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数的解析式为y=$\sqrt{2}$sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<k<1 | B. | k>1 | C. | k<-1 | D. | k<-1或k>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .[-3,3] | B. | [-2$\sqrt{3}$,2$\sqrt{3}$] | C. | [0,2$\sqrt{3}$] | D. | [-$\frac{1}{2}$,2$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com