
分析 (Ⅰ)将$M({1,\frac{{\sqrt{3}}}{2}})$及对应的参数$φ=\frac{π}{3}$,代入$\left\{\begin{array}{l}x=acosφ\\ y=bsinφ\end{array}\right.$,求出曲线C1的方程,设圆C2的半径为R,由题意,圆C2的方程为ρ=2Rcosθ,(或(x-R)2+y2=R2).由此能求出曲线C2的直角坐标方程.
(Ⅱ)由点A(ρ1,θ),$B({{ρ_2},θ+\frac{π}{2}})$在曲线C1上,能求出$\frac{1}{ρ_1^2}+\frac{1}{ρ_2^2}$的值.
解答 解:(Ⅰ)将$M({1,\frac{{\sqrt{3}}}{2}})$及对应的参数$φ=\frac{π}{3}$,代入$\left\{\begin{array}{l}x=acosφ\\ y=bsinφ\end{array}\right.$,
得$\left\{\begin{array}{l}1=acos\frac{π}{3}\\ \frac{{\sqrt{3}}}{2}=bsin\frac{π}{3}\end{array}\right.$,即$\left\{\begin{array}{l}a=2\\ b=1\end{array}\right.$,
所以曲线C1的方程为$\left\{\begin{array}{l}x=2cosφ\\ y=sinφ\end{array}\right.$(φ为参数),或$\frac{x^2}{4}+{y^2}=1$.
设圆C2的半径为R,由题意,圆C2的方程为ρ=2Rcosθ,(或(x-R)2+y2=R2).
将点$D({1,\frac{π}{3}})$代入ρ=2Rcosθ,得$1=2Rcos\frac{π}{3}$,即R=1.
(或由$D({1,\frac{π}{3}})$,得$D({\frac{1}{2},\frac{{\sqrt{3}}}{2}})$,代入(x-R)2+y2=R2,得R=1),
所以曲线C2的直角坐标方程为(x-1)2+y2=1.
(Ⅱ)因为点A(ρ1,θ),$B({{ρ_2},θ+\frac{π}{2}})$在曲线C1上,
所以$\frac{{ρ_1^2{{cos}^2}θ}}{4}+ρ_1^2{sin^2}θ=1$,$\frac{{ρ_2^2{{sin}^2}θ}}{4}+$$ρ_2^2{cos^2}θ=1$,
所以$\frac{1}{ρ_1^2}+\frac{1}{ρ_2^2}$=$({\frac{{{{cos}^2}θ}}{4}+{{sin}^2}θ})$$+({\frac{{{{sin}^2}θ}}{4}+{{cos}^2}θ})=\frac{5}{4}$.
点评 本题考查曲线的直角坐标方程、代数的和的求法,考查极坐标、直角坐标的互化,考查推理论证能力、运算求解能力,考查化归与转化思想,考查创新意识、应用意识,是中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | a、b都小于2 | B. | a、b至少有一个不小于2 | ||
| C. | a、b至少有两个不小于2 | D. | a、b至少有一个小于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
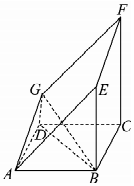 如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.
如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
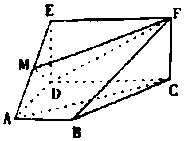 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{5}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com