
分析 求出公差,进而利用等差数列的性质可知S2017=-(a1+a3+…+a2017)+(a2+a4+…+a2016)=-$\frac{1}{2}$•(a1+a2017),进而计算可得结论
解答 解:依题意,d=$\frac{{a}_{5}-{a}_{1}}{4}$=3tan225°=3,
∴an=1+3(n-1)=3n-2,
∴S2017=-(a1+a3+…+a2017)+(a2+a4+…+a2016)
=-$\frac{1009}{2}$•(a1+a2017)+$\frac{1008}{2}$(a2+a2016)
=-$\frac{1009}{2}$•(a1+a2017)+$\frac{1008}{2}$(a1+a2017)
=-$\frac{1}{2}$•(a1+a2017)
=$-\frac{1}{2}$•(-1+3×2017-2)
=-3025,
故答案为:-3025
点评 本题考查数列的通项,注意解题方法的积累,属于中档题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
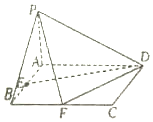 已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.
已知四棱锥P-ABCD底面ABCD是矩形,PA⊥平面ABCD,AD=4,AB=2,E,F分别是线段AB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com