
分析 (Ⅰ)由已知可得:圆心到直线x+y+b=0的距离为1,椭圆C经过点$(1,\frac{{2\sqrt{3}}}{3})$,列出方程组,求出a,b,由此能求出椭圆C的标准方程.
(Ⅱ)(1)设Q(x0,y0),M(x1,y1),N(x2,y2),OQ的方程为x=my,则MN的方程为x=my+1.由$\left\{\begin{array}{l}x=my\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$,得$|OQ|=\sqrt{1+{m^2}}•|{y_0}|$=$\frac{{\sqrt{6}\sqrt{1+{m^2}}}}{{\sqrt{2{m^2}+3}}}$,由$\left\{\begin{array}{l}x=my+1\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$,得(2m2+3)y2+4my-4=0,由此利用韦达定理、弦长公式,结合已知条件能求出$\frac{|MN|}{{|OQ{|^2}}}$的值为一个常数.
(2)△QF2M的面积=△OF2M的面积,从而S=S1+S2=S△OMN,求出O到直线MN:x=my+1的距离,结合已知条件能求出S的最大值.
解答 解:(Ⅰ)由已知可得:圆心到直线x+y+b=0的距离为1,即$\frac{b}{{\sqrt{2}}}=1$,所以$b=\sqrt{2}$,
又椭圆C经过点$(1,\frac{{2\sqrt{3}}}{3})$,所以$\frac{1}{a^2}+\frac{4}{{3{b^2}}}=1$,得到$a=\sqrt{3}$,
所以椭圆C的标准方程为$\frac{x^2}{3}+\frac{y^2}{2}=1$.
(Ⅱ)(1)设Q(x0,y0),M(x1,y1),N(x2,y2),OQ的方程为x=my,
则MN的方程为x=my+1.
由$\left\{\begin{array}{l}x=my\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$得$\left\{\begin{array}{l}{x^2}=\frac{{6{m^2}}}{{2{m^2}+3}}\\{y^2}=\frac{6}{{2{m^2}+3}}\end{array}\right.$即$\left\{\begin{array}{l}{x_0}^2=\frac{{6{m^2}}}{{2{m^2}+3}}\\{y_0}^2=\frac{6}{{2{m^2}+3}}.\end{array}\right.$
所以$|OQ|=\sqrt{1+{m^2}}•|{y_0}|$=$\frac{{\sqrt{6}\sqrt{1+{m^2}}}}{{\sqrt{2{m^2}+3}}}$,
由$\left\{\begin{array}{l}x=my+1\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$,得(2m2+3)y2+4my-4=0,
所以${y_1}+{y_2}=-\frac{4m}{{2{m^2}+3}}$,${y_1}{y_2}=-\frac{4}{{2{m^2}+3}}$,$|MN|=\sqrt{1+{m^2}}•|{y_1}-{y_2}|$=$\sqrt{1+{m^2}}•\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$
=$\sqrt{1+{m^2}}•\sqrt{\frac{{16{m^2}}}{{{{(2{m^2}+3)}^2}}}+\frac{16}{{2{m^2}+3}}}$=$\sqrt{1+{m^2}}•\frac{{4\sqrt{3}\sqrt{1+{m^2}}}}{{2{m^2}+3}}=\frac{{4\sqrt{3}(1+{m^2})}}{{2{m^2}+3}}$,
所以$\frac{|MN|}{{|OQ{|^2}}}=\frac{{\frac{{4\sqrt{3}(1+{m^2})}}{{2{m^2}+3}}}}{{\frac{{6(1+{m^2})}}{{2{m^2}+3}}}}=\frac{{2\sqrt{3}}}{3}$.
(2)∵MN∥OQ,∴△QF2M的面积=△OF2M的面积,∴S=S1+S2=S△OMN,
∵O到直线MN:x=my+1的距离$d=\frac{1}{{\sqrt{{m^2}+1}}}$,
∴$S=\frac{1}{2}|MN|•d=\frac{1}{2}×\frac{{4\sqrt{3}({m^2}+1)}}{{2{m^2}+3}}×\frac{1}{{\sqrt{{m^2}+1}}}=\frac{{2\sqrt{3}\sqrt{{m^2}+1}}}{{2{m^2}+3}}$,
令$\sqrt{{m^2}+1}=t$,则m2=t2-1(t≥1),$S=\frac{{2\sqrt{3}t}}{{2({t^2}-1)+3}}=\frac{{2\sqrt{3}t}}{{2{t^2}+1}}=\frac{{2\sqrt{3}}}{{2t+\frac{1}{t}}}$,
令$g(t)=2t+\frac{1}{t}(t≥1)$,$g'(t)=2-\frac{1}{t^2}>0$,
∴g(t)在[1,+∞)上为增函数,g(t)min=g(1)=3,${S_{max}}=\frac{{2\sqrt{3}}}{3}$.
点评 本题考查椭圆、直线方程、韦达定理、弦长公式、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
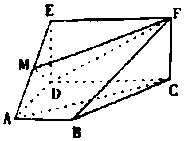 如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.
如图,四边形ABCD是梯形.四边形CDEF是矩形.且平面ABCD⊥平面CDEF,∠BAD=90°,AB∥CD,AB=AD=DE=$\frac{1}{2}$CD,M是线段AE上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com