
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
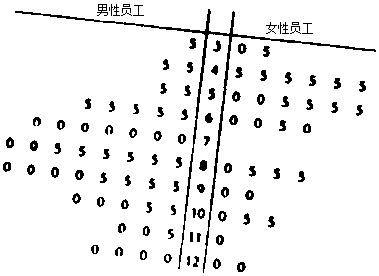
分析 (Ⅰ)120分钟时男性有4人,女性有2人,即可求2人中恰好有1名女性员工的概率;
(Ⅱ)根据所给数据完成2×2列联表,求出K2,与临界值比较,得出有99.9%以上的把握认为“喜爱春晚”与性别相关
解答 解:(Ⅰ)120分钟时男性有4人,女性有2人.
∴设2人中恰好有1名女性为事件A
∴P(A)=$\frac{{C}_{1}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{4}{15}$;
(Ⅱ)2×2列联表
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | 40 | 5 | 45 |
| 女性员工 | 16 | 14 | 30 |
| 合计 | 56 | 19 | 75 |
点评 本题考查概率的计算,考查独立性检验知识的运用,考查学生的计算能力,属于中档题.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
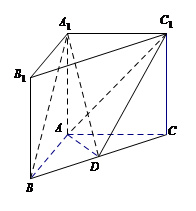 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
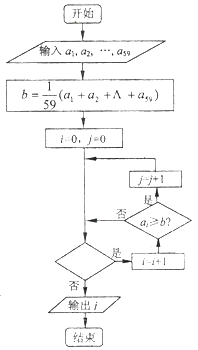 设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )
设计如图的程序框图,统计高三某班59位同学的数学平均分,输出不少于平均分的人数 (用j表示),则判断框中应填入的条件是( )| A. | i<58? | B. | i≤58? | C. | j<59? | D. | j≤59? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不大于2 | B. | 都小于2 | ||
| C. | 至少有一个不小于2 | D. | 都大于2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com