
| A. | 至少有一个不大于2 | B. | 都小于2 | ||
| C. | 至少有一个不小于2 | D. | 都大于2 |
分析 由x,y,z∈R+,a=x+$\frac{1}{y}$,b=y+$\frac{1}{z}$,c=z+$\frac{1}{x}$,则a,b,c三数至少有一个不小于2.利用反证法与基本不等式即可证明结论.
解答 解:由x,y,z∈R+,a=x+$\frac{1}{y}$,b=y+$\frac{1}{z}$,c=z+$\frac{1}{x}$,则a,b,c三数至少有一个不小于2.
下面利用反证法证明:假设a,b,c三数都小于2.
则6>a+b+c=x+$\frac{1}{y}$+y+$\frac{1}{z}$+z+$\frac{1}{x}$≥$2\sqrt{x•\frac{1}{x}}$+2$\sqrt{y•\frac{1}{y}}$+2$\sqrt{z•\frac{1}{z}}$=6,即6>6,矛盾.
因此原结论正确.
故选:C.
点评 本题考查了基本不等式的性质、反证法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
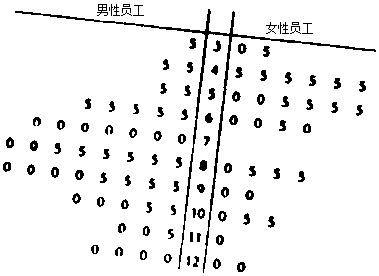
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
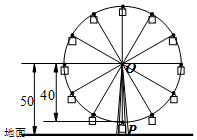 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
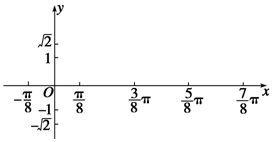 已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{b_1}{a_1}•\frac{b_2}{a_2}=-1$ | B. | a1a2+b1b2=0 | ||
| C. | $\frac{b_1}{a_1}=\frac{b_2}{a_2}$ | D. | a1b2=a2b1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com