
分析 (1)利用判别式△<0求出p为真时a的取值范围,根据指数函数的图象与性质求出q为真时a的取值范围;由p∨q是真命题且p∧q是假命题知p、q一真一假,由此求出a的范围;
(2)解不等式$\frac{2a-1}{a-2}≤1$得出命题r为真时a的取值范围,根据集合的包含关系判断命题?p是命题r成立的充分不必要条件.
解答 解:关于x的不等式x2+(a-1)x+a2≤0的解集为∅,
∴△=(a-1)2-4a2<0,
即3a2+2a-1>0,
解得a<-1或a>$\frac{1}{3}$,
∴p为真时a<-1或a>$\frac{1}{3}$;
又函数y=(2a2-a)x为增函数,
∴2a2-a>1,
即2a2-a-1>0,
解得a<-$\frac{1}{2}$或a>1,
∴q为真时a<-$\frac{1}{2}$或a>1;
(1)∵p∨q是真命题且p∧q是假命题,∴p、q一真一假,
∴当P假q真时,$\left\{\begin{array}{l}{-1≤a≤\frac{1}{3}}\\{a<-\frac{1}{2}或a>1}\end{array}\right.$,即-1≤a<-$\frac{1}{2}$;
当p真q假时,$\left\{\begin{array}{l}{a<-1或a>\frac{1}{3}}\\{-\frac{1}{2}≤a≤1}\end{array}\right.$,即$\frac{1}{3}$<a≤1;
∴p∨q是真命题且p∧q是假命题时,a的范围是-1≤a<-$\frac{1}{2}$或$\frac{1}{3}$<a≤1;
(2)∵$\frac{2a-1}{a-2}≤1$,
∴$\frac{2a-1}{a-2}$-1≤0,
即$\frac{a+1}{a-2}≤0$,
解得-1≤a<2,
∴a∈[-1,2),
∵?p为真时-1≤a≤$\frac{1}{3}$,
由[-1,$\frac{1}{3}$)是[-1,2)的真子集,
∴?p⇒r,且r≠>?p,
∴命题?p是命题r成立的一个充分不必要条件.
点评 本题考查了复合命题的真假性问题,也考查了不等式与函数的应用问题,是综合题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
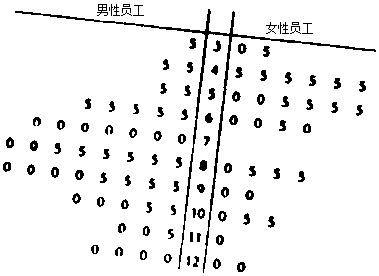
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 喜爱春晚 | 不喜爱春晚 | 合计 | |
| 男性员工 | |||
| 女性员工 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
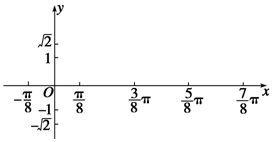 已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
已知曲线y=Asin(ωx+φ) (A>0,ω>0)上的一个最高点的坐标为($\frac{π}{8}$,$\sqrt{2}$),此点到相邻最低点间的曲线与x轴交于点 ($\frac{3}{8}$π,0),若φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com