
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{5}}}{2}$ | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
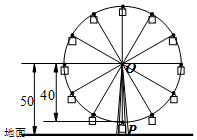 如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
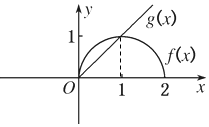 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-2,2],且它们在x∈[0,2]上图象如图所示,f(x)>g(x)的解集是( )| A. | [-2,0)∪(0,1) | B. | (0,1) | C. | [-2,0) | D. | (-2,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com