
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
分析 (1)由全部105人中抽到随机抽取1人为优秀的概率为$\frac{2}{7}$,我们可以计算出优秀人数为30,我们易得到表中各项数据的值.
(2)找出满足条件抽到6或10号的基本事件个数,及总的基本事件的个数,再代入古典概型公式进行计算求解.
解答 解:(1)∵全部105人中抽到随机抽取1人为优秀的概率为$\frac{2}{7}$,
∴我们可以计算出优秀人数为$\frac{2}{7}$×105=30,得乙班优秀人数30-10=20,列联表为:
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
点评 本题考查列联表,考查古典概型概率的计算,考查学生分析解决问题的能力,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
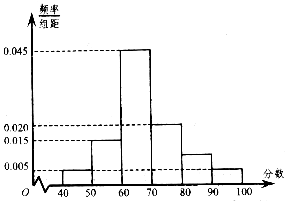 上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.
上周某校高三年级学生参加了数学测试,年部组织任课教师对这次考试进行成绩分析.现从中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);…;第六组[90,100],并据此绘制了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:5 | B. | 9:25 | C. | 5:$\sqrt{41}$ | D. | 7:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com