
| A. | $±\frac{{\sqrt{5}}}{2}$ | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
分析 由已知AB与x轴交于点F2,设∠AOF2=α,则$tanα=\frac{b}{a}$,△AOB中,可得$tan2α=\frac{4}{3}$,$tanα=\frac{1}{2}$,即可求出双曲线的渐近线斜率.
解答 解:由已知AB与x轴交于点F2,设∠AOF2=α,
则$tanα=\frac{b}{a}$,△AOB中,可得$tan2α=\frac{4}{3}$,
设|OA|=m-d、|AB|=m、|OB|=m+d,
∵OA⊥BF,∴(m-d)2+m2=(m+d)2,
整理,得d=$\frac{1}{4}$m,△AOB中,∠AOB=2α,tan∠AOB=tan2α=$\frac{|AB|}{|OA|}$=$\frac{4}{3}$
∴$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{4}{3}$,∴$tanα=\frac{1}{2}$,
∴双曲线的渐近线斜率为$±\frac{1}{2}$.
故选D.
点评 本题考查了双曲线的简单性质,考查学生的计算能力,属于中档题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:5 | B. | 9:25 | C. | 5:$\sqrt{41}$ | D. | 7:9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2 | B. | 2:5 | C. | 1:3 | D. | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
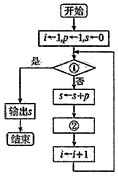 给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),
给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | kx+y+k=0 | B. | kx-y-1=0 | C. | kx+y-k=0 | D. | kx+y-2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com