
| A. | kx+y+k=0 | B. | kx-y-1=0 | C. | kx+y-k=0 | D. | kx+y-2=0 |
分析 对于A,k=-1时,直线l和直线kx+y+k=0关于x轴对称,则此时它们所截的弦长相等,故不能选 A.
对于B,直线l和直线kx-y-1=0平行且它们所截得的弦长相等,
对于C,k=-1时,直线l和直线kx+y-k=0关于y轴对称,则此时它们所截的弦长相等,
对于D:直线kx+y-2=0的斜率为-k,在y轴上的截距为2,这两直线不关于x轴、y轴、原点对称,故被椭圆E所截得的弦长不可能相等.
解答 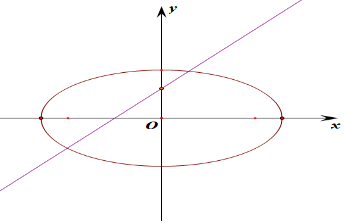 解:对于A,k=-1时,直线l和直线kx+y+k=0关于x轴对称,则此时它们所截的弦长相等,则A选项错误;
解:对于A,k=-1时,直线l和直线kx+y+k=0关于x轴对称,则此时它们所截的弦长相等,则A选项错误;
对于B,直线l和直线kx-y-1=0平行且它们所截得的弦长相等,则B选项错误;
对于C,k=-1时,直线l和直线kx+y-k=0关于y轴对称,则此时它们所截的弦长相等,则C选项错误;
对于D:直线l斜率为k,在y轴上的截距为1,直线kx+y-2=0的斜率为-k,在y轴上的截距为2,这两直线不关于x轴、y轴、原点对称,
故被椭圆E所截得的弦长不可能相等.
故选:D.
点评 本题考查直线和椭圆的位置关系,通过给变量取特殊值,举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $±\frac{{\sqrt{5}}}{2}$ | B. | ±2 | C. | $±\sqrt{2}$ | D. | $±\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与第几次抽样无关,每次抽中的可能性相等 | |
| B. | 与第几次抽样无关,第一次抽中的可能性要大些 | |
| C. | 与第几次抽样有关,最后一次抽中的可能性大些 | |
| D. | 与第几次抽样有关,虽然每次都是等可能的抽取,但各次抽取的可能性不一样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2})$ | B. | (1,2) | C. | $(\sqrt{2},\sqrt{3})$ | D. | $(\sqrt{3},2)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com