
分析 对函数f(x)进行求导,然后令导函数大于0,得出原函数增区间,令导函数小于0,得出原函数的减区间.
解答 解:f(x)=x(ex-1)-$\frac{1}{2}$x2,
f′(x)=xex+ex-x-1=(x+1)(ex-1),
令f′(x)=0,解得:x1=-1,x2=0,
令f′(x)>0,解得:x<-1或x>0,
函数在(-∞,-1),(0,+∞)上单调递增,
令f′(x)<0,解得:-1<x<0,
函数在(-1,0)上单调递减,
总上可知:f(x)的单调递增区间为:(-∞,-1),(0,+∞),
单调递减区间:(-1,0).
点评 本题考查利用导数研究函数的单调性,考查不等式的解法,注意解题方法的积累,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
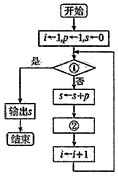 给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),
给出30个数:1,2,4,7,…其规律是:第一个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这30个数的和,现已给出了该问题算法的程序框图(如图所示),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
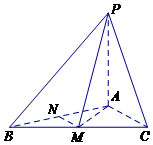 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | kx+y+k=0 | B. | kx-y-1=0 | C. | kx+y-k=0 | D. | kx+y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com