
分析 方法一:求导,求得直线PA的方程,将P代入直线方程,求得x12-2ax1-8,同理可知x22-2ax2-8=0.则x1,x2是方程x2-2ax-8=0的两个根,则由韦达定理求得x1x2,y1y2的值,即可求证x1x2+y1y2为定值;
方法二:设切线方程,代入抛物线方程,由△=0,则k1k2=-2,分别求得切线方程,代入即可求证x1x2+y1y2为定值.
解答 证明:方法一:由x2=4y,得y=$\frac{1}{4}$x2,求导y′=$\frac{1}{2}$x.
则直线PA的斜率为$\frac{1}{2}$x1.
由点A(x1,y1)和B(x2,y2)在抛物线C上,所以y=$\frac{1}{4}$x12,y=$\frac{1}{4}$x22.
∴直线PA的方程为y-$\frac{1}{4}$x12=$\frac{1}{2}$x1(x-x1).
∵点P(a,-2)在直线PA上,
∴-2-$\frac{1}{4}$x12=$\frac{1}{2}$x1(a-x1),即x12-2ax1-8=0.
同理,x22-2ax2-8=0.
∴x1,x2是方程x2-2ax-8=0的两个根.
∴x1x2=-8.…(4分)
又y1y2=$\frac{1}{4}$x12×$\frac{1}{4}$x22=4,
∴x1x2+y1y2=-4为定值.
方法二:设过点P(a,-2)且与抛物线C相切的切线方程为y+2=k(x-a),
$\left\{\begin{array}{l}{y+2=k(x-a)}\\{{x}^{2}=4y}\end{array}\right.$,消去y得x2-4kx+4ka+8=0,
由△=16k2-4(4ak+8)=0,化简得k2-ak-2=0.
∴k1k2=-2.…(3分)
由x2=4y,得y=$\frac{1}{4}$x2,求导y′=$\frac{1}{2}$x.
则直线PA的斜率为k1=$\frac{1}{2}$x1.,直线PB的斜率为k2=$\frac{1}{2}$x2.
∴$\frac{1}{4}$x1x2=-2,即x1x2=-8.…(4分)
又y1y2=$\frac{1}{4}$x12×$\frac{1}{4}$x22=4,
∴x1x2+y1y2=-4为定值.
∴x1x2+y1y2为定值-4.
点评 本题考查直线与抛物线的位置关系,考查导数的几何意义,韦达定理,直线的斜率公式,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 12$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {α|α=k•360°+300°,k∈Z} | B. | {α|α=k•360°+60°,k∈Z} | ||
| C. | {α|α=k•360°+30°,k∈Z} | D. | {α|α=k•360°-60°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin4x | B. | y=cos2x | C. | y=tan2x | D. | $y=sin(\frac{π}{2}-4x)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
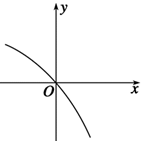 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )| A. | (1,6) | B. | (-1,5) | C. | (0,5) | D. | (3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com