
分析 (1)设点M的坐标是(x,y),点P的坐标是(x0,y0),由点Q的坐标是(4,0),点M是线段PQ的中点,推导出点P的坐标满足方程(x0+2)2+${{y}_{0}}^{2}$=4,由此能求出点M的轨迹方程.
(2)设直线AC的斜率为k1(k1>0),直线BC的斜率为k2(k2≤0),则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.由方程组$\left\{\begin{array}{l}{y={k}_{1}x+t}\\{y={k}_{2}x+t+6}\end{array}\right.$,得C点的横坐标为$\frac{6}{{k}_{1}-{k}_{2}}$.从而S=$\frac{18}{{{k_1}-{k_2}}}$.,点M的轨迹为圆N,从而点M的轨迹与△ABC内切,圆N与直线AC、BC都相切,由此能求出结果.
解答 解:(1)设点M的坐标是(x,y),点P的坐标是(x0,y0),
由于点Q的坐标是(4,0),且点M是线段PQ的中点,
所以$\left\{\begin{array}{l}{x=\frac{{x}_{0}+4}{2}}\\{y=\frac{{y}_{0}}{2}}\end{array}\right.$,于是有$\left\{\begin{array}{l}{{x}_{0}=2x-4}\\{{y}_{0}=2y}\end{array}\right.$,①…(2分)
因为点P在圆(x+2)2+y2=4上运动,
所以点P的坐标满足方程(x+2)2+y2=4,即(x0+2)2+${{y}_{0}}^{2}$=4,②
把①代入②得(2x-4+2)2+(2y)2=4,整理得(x-1)2+y2=1,
∴点M的轨迹方程是(x-1)2+y2=1,…(4分)
它是以N(1,0)为圆心,半径长为1的圆. …(5分)
(2)设直线AC的斜率为k1(k1>0),直线BC的斜率为k2(k2≤0),
则直线AC的方程为y=k1x+t,直线BC的方程为y=k2x+t+6.
由方程组$\left\{\begin{array}{l}{y={k}_{1}x+t}\\{y={k}_{2}x+t+6}\end{array}\right.$,解得C点的横坐标为$\frac{6}{{k}_{1}-{k}_{2}}$. …(6分)
∵|AB|=t+6-t=6,
∴S=$\frac{1}{2}$×|$\frac{6}{{k}_{1}-{k}_{2}}$|×6=$\frac{18}{|{k}_{1}-{k}_{2}|}$=$\frac{18}{{{k_1}-{k_2}}}$. …(7分)
由(1)知点M的轨迹为圆N,∴点M的轨迹与△ABC相切,即圆N与△ABC内切,
∴圆N与直线AC、BC都相切,
∴1=$\frac{|{k}_{1}+t|}{\sqrt{1+{{k}_{1}}^{2}}}$,∴k1=$\frac{1-t2}{2t}$;
同理可得${k}_{2}=\frac{1-(t+6)^{2}}{2(t+6)}$. …(8分)
∴k1-k2=$\frac{3({t}^{2}+6t+1)}{{t}^{2}+6t}$,
∴S=$\frac{6({t}^{2}+6t)}{{t}^{2}+6t+1}$=6(1-$\frac{1}{{t}^{2}+6t+1}$),…(9分)
∵-5≤t≤-2,∴-8≤t2+6t+1≤-4,
∴Smax=6×(1+$\frac{1}{4}$)=$\frac{15}{2}$,Smin=6×(1+$\frac{1}{8}$)=$\frac{27}{4}$. …(10分)
点评 本题考查点的轨迹方程的求法,考查三角形面积的最大值和最小值的求法,涉及到直线方程、圆、直线与圆相切等知识点,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| a | b | c | d | |
| r | 0.80 | 0.76 | 0.67 | 0.82 |
| m | 100 | 113 | 121 | 99 |
| A. | a | B. | b | C. | c | D. | d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
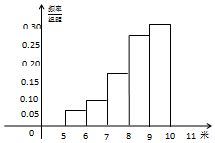 某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.
某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据整理后,分成六组得到频率分布直方图的一部分(如图).已知前五个小组的频率分别为0.06.0.10,0.14,0.28,0.30.第六小组的频数是6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2<b2 | B. | a2b<ab2 | C. | D.$\frac{1}{a}$>$\frac{1}{b}$ | D. | 2a-2b<0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com