
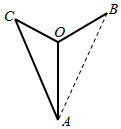
 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.分析 (1)根据条件结合余弦定理建立函数关系即可求y关于x的函数关系式,并写出x的取值范围;
(2)求出N-M的表达式,利用换元法结合基本不等式的性质即可求出N-M的最大值及相应的x的值.
解答 解:(1)∵OA=x,OB=y,AB=y+1,
由余弦定理得x2+y2-2xycos120°=(y+1)2,解得y=$\frac{{x}^{2}-1}{2-x}$,
由x>0,y>0,得1<x<2,
∵x>y,
∴x>$\frac{{x}^{2}-1}{2-x}$,
得1<x<$\frac{1+\sqrt{3}}{2}$,
∴OA的取值范围是(1,$\frac{1+\sqrt{3}}{2}$).
(2)M=kOB=ky,N=4$\sqrt{3}$k•S△AOC=3kx,
则N-M=k(3x-y)=k(3x-$\frac{{x}^{2}-1}{2-x}$),
设2-x=t,则t∈($\frac{3-\sqrt{3}}{3}$,1),
则N-M=k[3(2-t)-$\frac{(2-t)^{2}-1}{t}$]=k[10-(4t+$\frac{3}{t}$)]≤k(10-2$\sqrt{4t•\frac{3}{t}}$)=(10-4$\sqrt{3}$)k,
当且仅当4t=$\frac{3}{t}$,即t=$\frac{\sqrt{3}}{2}$,x=2-$\frac{\sqrt{3}}{2}$时,N-M的最大值是)=(10-4$\sqrt{3}$)k.
点评 本题主要考查函数解析式的求解以及函数最值的应用,利用余弦定理结合换元法,以及基本不等式的应用是解决本题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com