
分析 (1)双曲线3x2-y2=3即${x}^{2}-\frac{{y}^{2}}{3}$=1的离心率e=2.由题意可得:椭圆的离心率$e=\frac{1}{2}$=$\frac{c}{a}$,b2=a2-c2,把点$(1,\frac{3}{2})$代入椭圆方程解出即可得出.
(2)设M(x1,y1),N(x2,y2),直线方程与椭圆方程联立消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,可得△>0,利用根与系数的关系及其中点坐标公式可得:MN中点P的坐标为$(-\frac{4km}{{3+4{k^2}}},\frac{3m}{{3+4{k^2}}})$,设MN的垂直平分线l′方程:$y=-\frac{1}{k}(x-\frac{1}{5})$,由于P在l′上可得:4k2+5km+3=0,与△>0联立解出即可得出.
解答 解:(1)双曲线3x2-y2=3即${x}^{2}-\frac{{y}^{2}}{3}$=1的离心率e=$\sqrt{1+\frac{3}{1}}$=2.
由题意可得:椭圆的离心率$e=\frac{1}{2}$.
∴$\frac{c}{a}=\frac{1}{2}$,∴a=2c,∴b2=a2-c2=3c2,
∴椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$…(2分)
又点$(1,\frac{3}{2})$在椭圆上,∴$\frac{1}{{4{c^2}}}+\frac{{{{(\frac{3}{2})}^2}}}{{3{c^2}}}=1$,∴c2=1,
∴椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$…(4分)
(2)设M(x1,y1),N(x2,y2),
由$\left\{{\begin{array}{l}{\frac{x^2}{4}+\frac{y^2}{3}=1}\\{y=kx+m}\end{array}}\right.$,消去y并整理得(3+4k2)x2+8kmx+4m2-12=0,
∵直线y=kx+m与椭圆有两个交点,△=(8km)2-4(3+4k2)(4m2-12)>0,即m2<4k2+3,…(6分)
又${x_1}+{x_2}=-\frac{8km}{{3+4{k^2}}}$,
∴MN中点P的坐标为$(-\frac{4km}{{3+4{k^2}}},\frac{3m}{{3+4{k^2}}})$,
设MN的垂直平分线l′方程:$y=-\frac{1}{k}(x-\frac{1}{5})$,
∴P在l′上$\frac{3m}{{3+4{k^2}}}=-\frac{1}{k}(-\frac{4km}{{3+4{k^2}}}-\frac{1}{5})$,即4k2+5km+3=0,$m=-\frac{{4{k^2}+3}}{5k}$,…(10分)
将上式代入得$\frac{{{{(4{k^2}+3)}^2}}}{{25{k^2}}}<4{k^2}+3$,${k^2}>\frac{1}{7}$,$k>\frac{{\sqrt{7}}}{7}$或$k<-\frac{{\sqrt{7}}}{7}$,
∴k的取值范围为$(-∞,-\frac{{\sqrt{7}}}{7})∪(\frac{{\sqrt{7}}}{7},+∞)$…(12分)
点评 本题考查了椭圆的定义标准方程及其性质、线段的垂直平分线的性质、一元二次方程的根与系数的关系、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
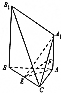 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2015 | B. | 2015 | C. | 0 | D. | 2014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
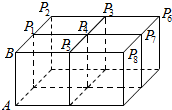 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
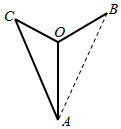 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com