
分析 (1)利用向量模的计算公式、二次函数的单调性即可得出;
(2)$cos<\overrightarrow{c},\overrightarrow{a}>$=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}$=$\frac{1-3λ+2(2+4λ)}{\sqrt{5}×\sqrt{25{λ}^{2}+10λ+5}}$=$\frac{λ+1}{\sqrt{5{λ}^{2}+2λ+1}}$,令f(λ)=$\frac{(λ+1)^{2}}{5{λ}^{2}+2λ+1}$,化简利用函数的性质即可得出.
解答 解:(1)$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$=(1-3λ,2+4λ),
∴|$\overrightarrow{c}$|=$\sqrt{(1-3λ)^{2}+(2+4λ)^{2}}$=$\sqrt{25{λ}^{2}+10λ+5}$=$\sqrt{25(λ+\frac{1}{5})^{2}+4}$≥2,当$λ=-\frac{1}{5}$时取等号,
∴|$\overrightarrow{c}$|最小时的λ=-$\frac{1}{5}$.
(2)$cos<\overrightarrow{c},\overrightarrow{a}>$=$\frac{\overrightarrow{a}•\overrightarrow{c}}{|\overrightarrow{a}||\overrightarrow{c}|}$=$\frac{1-3λ+2(2+4λ)}{\sqrt{5}×\sqrt{25{λ}^{2}+10λ+5}}$=$\frac{λ+1}{\sqrt{5{λ}^{2}+2λ+1}}$,
令f(λ)=$\frac{(λ+1)^{2}}{5{λ}^{2}+2λ+1}$,f(-1)=0,$f(-\frac{1}{2})$=$\frac{1}{5}$,f(0)=1.
λ≠-1,-$\frac{1}{2}$,0时,f(λ)=$\frac{1}{5}$+$\frac{4}{5}$•$\frac{1}{\frac{5{λ}^{2}+2λ+1}{2λ+1}}$,
令g(λ)=$\frac{5{λ}^{2}}{2λ+1}$=$\frac{5}{(\frac{1}{λ}+1)^{2}-1}$∈(-∞,-5)∪(0,+∞).
∴f(λ)∈[0,1],
∴$cos<\overrightarrow{c},\overrightarrow{a}>$∈[-1,1].
点评 本题考查了向量夹角公式、向量模的计算公式、二次函数的单调性、函数的性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
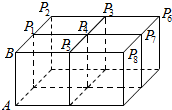 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
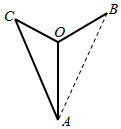 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b | B. | a-b | C. | $\frac{a+b}{2}$ | D. | $\frac{a-b}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,11] | B. | [1,13] | C. | [5-2$\sqrt{21}$,5+2$\sqrt{21}$] | D. | [7-2$\sqrt{21}$,7+2$\sqrt{21}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com