
分析 求解定积分得到a值,代入函数解析式,求其导函数,取x=2即可得到曲线y=ax2在x=2处切线的斜率,运用基本不等式即可得到所求最小值.
解答 解:a≥$\frac{4}{3}$${∫}_{0}^{\frac{π}{6}}$cosθdθ=$\frac{4}{3}$•sinθ|${\;}_{0}^{\frac{π}{6}}$=$\frac{4}{3}$×(sin$\frac{π}{6}$-sin0)=$\frac{2}{3}$,
可得a-$\frac{1}{2}$≥$\frac{2}{3}$-$\frac{1}{2}$=$\frac{1}{6}$,
f(x)=ax+$\frac{2}{a}$ln(ax-1)的导数为f′(x)=a+$\frac{2}{a}$•a•$\frac{1}{ax-1}$=a+$\frac{2}{ax-1}$,
在点(2,f(2))处切线的斜率为k=a+$\frac{2}{2a-1}$=(a-$\frac{1}{2}$)+$\frac{1}{a-\frac{1}{2}}$+$\frac{1}{2}$
≥2$\sqrt{(a-\frac{1}{2})•\frac{1}{a-\frac{1}{2}}}$+$\frac{1}{2}$=$\frac{5}{2}$.
当且仅当a=$\frac{3}{2}$时,取得最小值$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了定积分,考查了利用导数研究过曲线上某点处的切线方程,在曲线上某点处的切线的斜率,就是函数在该点处的导数值,考查基本不等式的运用,是中档题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{6}$,kπ+$\frac{π}{3}$](k∈Z) | D. | [kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
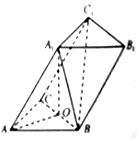 如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=60°,∠A1AC=∠A1AB,AA1=AB=AC=2,点O是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com