
【题目】已知函数![]()
(1)若![]() ,函数
,函数![]() 的极大值为
的极大值为![]() ,求实数
,求实数![]() 的值;
的值;
(2)若对任意的![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)第(1)问,先求导,对a分类讨论,求出每一种情况下的极大值,得到a的方程,即可求出实数a的值. (2)第(2)问,令![]() ,转化成证明g(a)的最大值小于等于
,转化成证明g(a)的最大值小于等于![]() 在
在![]() 上恒成立,再分离参数
上恒成立,再分离参数![]() 对
对![]() 恒成立
恒成立![]() ,再利用导数求右边函数的最大值得解.
,再利用导数求右边函数的最大值得解.
试题解析:
(1)∵![]() ,
,
∴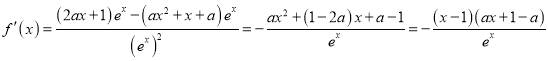
①当![]() 时,
时, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() 上单调递减.
上单调递减.
所以![]() 的极大值为
的极大值为![]() ,不合题意.
,不合题意.
②当![]() 时,
时, ![]() ,
,
令![]() ,得
,得![]() ;
; ![]() ,得
,得![]() 或
或![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增, ![]() 和
和![]() 上单调递减.
上单调递减.
所以![]() 的极大值为
的极大值为![]() ,解得
,解得![]() .符合题意.
.符合题意.
综上可得![]() .
.
(2)令![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上是增函数
上是增函数
则![]() 对
对![]() 恒成立等价于
恒成立等价于![]() ,
,
即![]() 对
对![]() 恒成立.
恒成立.
即![]() 对
对![]() 恒成立
恒成立![]()
令![]()
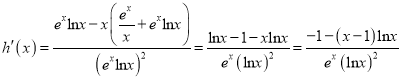
![]()
![]()
![]()
![]() 在
在![]() 上单调递减。
上单调递减。![]()
![]()
所以实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某公司拟购买一块地皮建休闲公园,如图,从公园入口![]() 沿
沿![]() ,
,![]() 方向修建两条小路,休息亭
方向修建两条小路,休息亭![]() 与入口的距离为
与入口的距离为![]() 米(其中
米(其中![]() 为正常数),过
为正常数),过![]() 修建一条笔直的鹅卵石健身步行带,步行带交两条小路于
修建一条笔直的鹅卵石健身步行带,步行带交两条小路于![]() 、
、![]() 处,已知
处,已知![]() ,
,![]() .
.

(1)设![]() 米,
米,![]() 米,求
米,求![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
(2)试确定![]() ,
,![]() 的位置,使三条路围成的三角形
的位置,使三条路围成的三角形![]() 地皮购价最低.
地皮购价最低.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是正方体的平面展开图,在这个正方体中,有以下四个命题:①![]() 平面ADNE;②
平面ADNE;②![]() 平面ABFE;③平面
平面ABFE;③平面![]() 平面AFN;④平面
平面AFN;④平面![]() 平面NCF.其中正确命题的序号是( )
平面NCF.其中正确命题的序号是( )
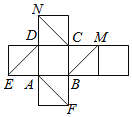
A.②③B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线与
的准线与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作圆
作圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,且
,且![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过定点
两点,过定点![]() 作
作![]() 的垂线与抛物线交于
的垂线与抛物线交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
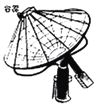
【题目】如图是一种加热食物的太阳灶,上面装有可旋转的抛物面形的反光镜,镜的轴截面是抛物线的一部分,盛食物的容器放在抛物线的焦点处,容器由若干根等长的铁筋焊接在一起的架子支撑.已知镜口圆的直径为8m,镜深1m.
(1)建立适当的坐标系,求抛物线的方程和焦点的位置;
(2)若把盛水和食物的容器近似地看作点,试求每根铁筋的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前n项和为
的前n项和为![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() .
.
(1)求![]() ,
,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)令![]() 问是否存在正数m,使得
问是否存在正数m,使得![]() 对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
对一切正整数n都成立?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站退出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组
.现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
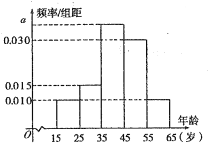
(1)求出![]() 的值;
的值;
(2)求这200人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(3)现在要从年龄较小的第1,2组中用分层抽样的方法抽取5人,再从这5人中随机抽取3人进行问卷调查,求这2组恰好抽到2人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com