
| A. | y=|x| | B. | y=log2|x| | C. | $y={|x|^{\frac{1}{2}}}$ | D. | y=0.5|x| |
分析 根据函数单调性的性质进行判断即可.
解答 解:y=|x|=$\left\{\begin{array}{l}{x,}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$则函数在(-∞,0)上为减函数,
y=log2x的定义域为(0,+∞),在(-∞,0)上无意义,不满足条件.
y=|x|${\;}^{\frac{1}{2}}$═$\sqrt{|x|}$定义域为(-∞,+∞),在(-∞,0)上为减函数,不满足条件.
当x<0时,y=0.5|x|=0.5-x=2x(,在(-∞,0)上单调递增,满足条件.
故选:D
点评 本题主要考查函数单调性的判断,要求熟练掌握常见函数的单调性的性质是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 4$-2\sqrt{2}$ | D. | 4$+2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
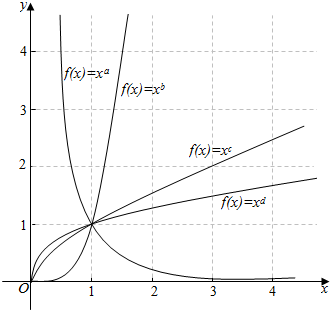
| A. | a+b+c+d为正数 | B. | b+c+d-a可能为零 | ||
| C. | a-b-c-d为负数 | D. | b×c×d×a符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 4 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
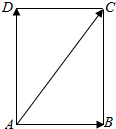 一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.
一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com